3.3 Fundamentals of Finance: Cashflow Models, Time Value of Money, and Interest Rates

Understanding cashflow models, the time value of money, and interest rates is essential in finance and investment.

Cashflow models provide a framework for analyzing the inflows and outflows of cash over time, enabling informed decision-making in resource allocation, project evaluation, and financial planning. However, cashflows are not equal across time due to the time value of money principle, which asserts that a dollar today is worth more than a dollar in the future due to its potential earning capacity if invested. This principle underscores the importance of considering the timing of cashflows and the associated opportunity cost in financial decision-making.

Interest rates play a pivotal role in determining the time value of money, representing the cost of borrowing or the return on investment. They significantly influence the present and future value of cashflows, whether it’s the interest earned on savings accounts, the cost of borrowing for a mortgage, or the discount rate used in cashflow models.

Understanding interest rates is crucial for assessing investment opportunities, managing debt, and evaluating the attractiveness of financial instruments.

In essence, cashflow models, the time value of money, and interest rates are interconnected concepts that form the foundation of financial analysis and decision-making.

Example 3.5: Illustrating Cashflows and Timeline

Explore how cashflows can be visually represented and understood through a timeline. Consider the following cashflow:

A series of payments into and out of a bank account is given as follows:

• payments into the account : ฿1000 on 1 January 2014 and ฿100 on 1 January 2016

• payments out of the account : ฿200 on 1 July 2015, ฿300 on 1 July 2016, and ฿400 on 1 January 2018

In practice, cashflows can be represented by a timeline as can be illustrated in this example.

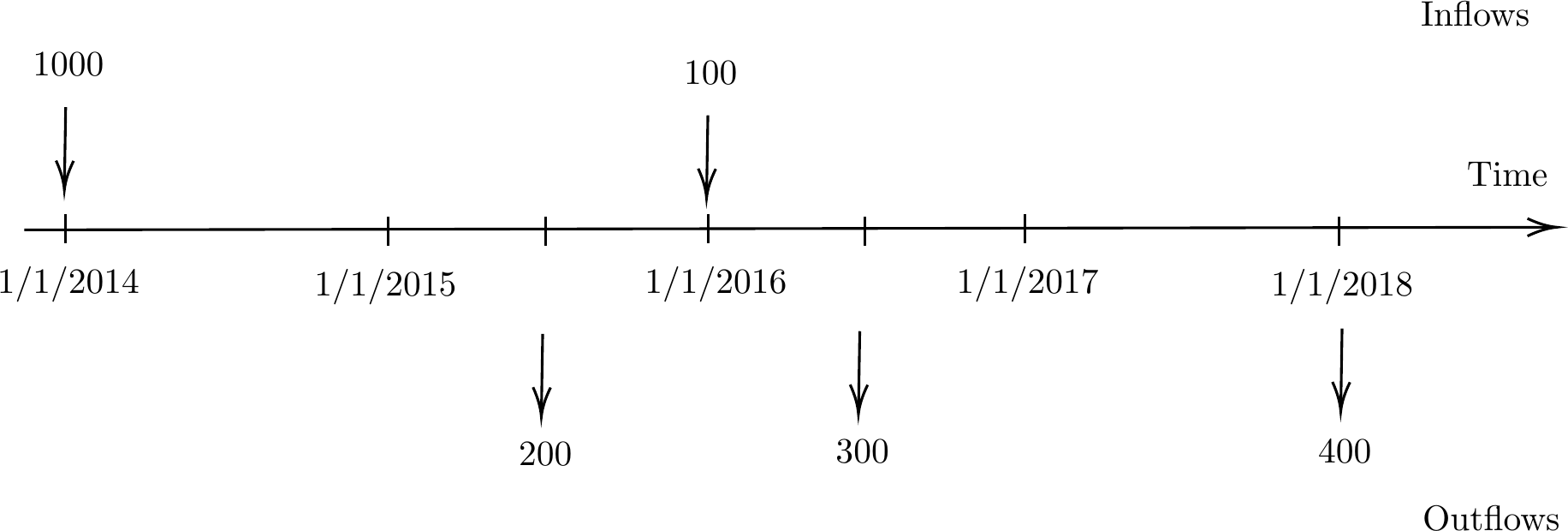
Fig. 9 an example of a timeline

Interest and the Time Value of Money

This section introduces the time value of money using the concepts of compound interest and discounting. The effect of interest rates on the present value of future cash flows is discussed. The value of distant cash flows in the present and current cash flows in the future are then considered.

We illustrate the time value of money by considering the following examples.

Example 3.6

An investor want to make a payment of ฿10000 in 2 years. Suppose that a bank pays compound interest at 4% per annum effective. How much should the initial investment?

Note The amount we need to invest now (i.e. the initial investment in this example) is called the present value (PV) or discounted value of the payments.

Solution to Example 3.6

Click to toggle answer

By the end of 2 years an initial payment of \textbaht X will have accumulated to:

\[ X \cdot 1.04^2 = 10000. \]

Hence, \(X = 9245.56 \).

Example 3.7: Time Value of Money

Consider the following arguments

• It is obvious that you would prefer to have ฿1100 now than ฿1000 now.

• If we receive and hold ฿1 now, then it is worth more than receiving and holding ฿1 at some time in the future? Why is this?

• Is it obvious that your would be better off with ฿1100 in 2 years than ฿1000 now?

Solution to Example 3.7

Click to toggle answer

For the second argument, this one baht will grow to \(1 + r\) in the first year, \((1 + r)^2\) in two years, and so on. These amounts are clearly worth more than receiving and holding ฿1 at the same time in the future.

For the last argument, we need to compare the values of the amounts received at different times. To do this, we can look at the today’s values of ฿1100 received in 2 years assuming that we can invest at an annual interest rate of \(r\) percent.

The present value of this amount \(X\) in year 2 is

\[1100/(1 + r)^2.\]

Assuming \(r = 5\%\), the present value of \(X\) is \(997.73\).

Comparing the values in today’s baths, it is better to have ฿1000 now than to have ฿1100 in 2 years.

Tip

From the above example,

1. One can deposit or invest ฿1 now and will receive ฿1 back and a reward called interest at some point in the future. Because of its potential earning power, money in the present is worth more than an equal amount in the future. This is a fundamental financial principle known as the time value of money.

2. At a given point of time, cash has a monetary value, but also has a time value.

3. The amount deposited or invested is called capital or principal.

Simple interest

Simple interest is a calculation of interest that does not take into account the effect of compounding. Under simple interest, the amount of interest that accrues over time is proportional to the length of the period.

Suppose an amount \(C\) is deposited in an account that pays simple interest at the rate of \(i\)% per annum. Then after \(n\) years the deposit will have accumulated to

\[C( 1 + i \cdot n).\]

Hence, the interest accrued over \(n\) years is

\[\text{Simple Interest} = C \cdot i \cdot n.\]

Note Auto loans and short-term personal loans are usually simple interest loans.

Example 3.8: Simple Interest

An investor deposits ฿10000 in a bank account that pays simple interest at a rate of 5% per annum. Calculate

1. interest he will earn after the first two years.

2. interest he will earn after the first three months.

Note When \(n\) is not an integer, interest is paid on a pro-rate basis (in proportion).

Solution to Example 3.8

Click to toggle answer

1. At the end of 2 years the interest earned is

   \[10000 \cdot 0.05 \cdot 2 = 1000.\]

2. At the end of 3 months the interest earned is

   \[10000 \cdot 0.05 \cdot \frac{3}{12} = 125.\]

   Alternatively, the interest per month is 5%/12 = 0.4167% and hence the interest earned can be calculated as

   \[10000 \cdot 0.004167 \cdot 3 = 125.\]

Compound interest

Compound interest refers to the interest that’s calculated on the initial principal, as well as on the accumulated interest from previous periods. In other words, it’s interest on interest. When interest is compounded, the interest earned in each period is added to the principal amount, and subsequent interest is calculated based on the new principal. Compound interest can lead to exponential growth of an investment or debt over time.

In compound interest, the accumulated amount over a period of time is the capital of the following period. Therefore, a capital of 1 unit at the end of the year increases to \(1 + i\) units, which becomes the capital for the following year.

For year 2, the principal is \(1 + i\) and the interest for the year is \(( 1 + i ) \cdot i\). By the end of 2 years, an initial payment of 1 will have accumuulated to

\[ (1+i) + ( 1 + i ) \cdot i = (1+i)^2.\]

As this progression continues, the accumulated amount of \(X\) units at the end of year \(n\) becomes

\[ X\cdot(1 + i)^n. \]

Note In this case, we can take money out and reinvest it as new capital illustrated in the timeline.

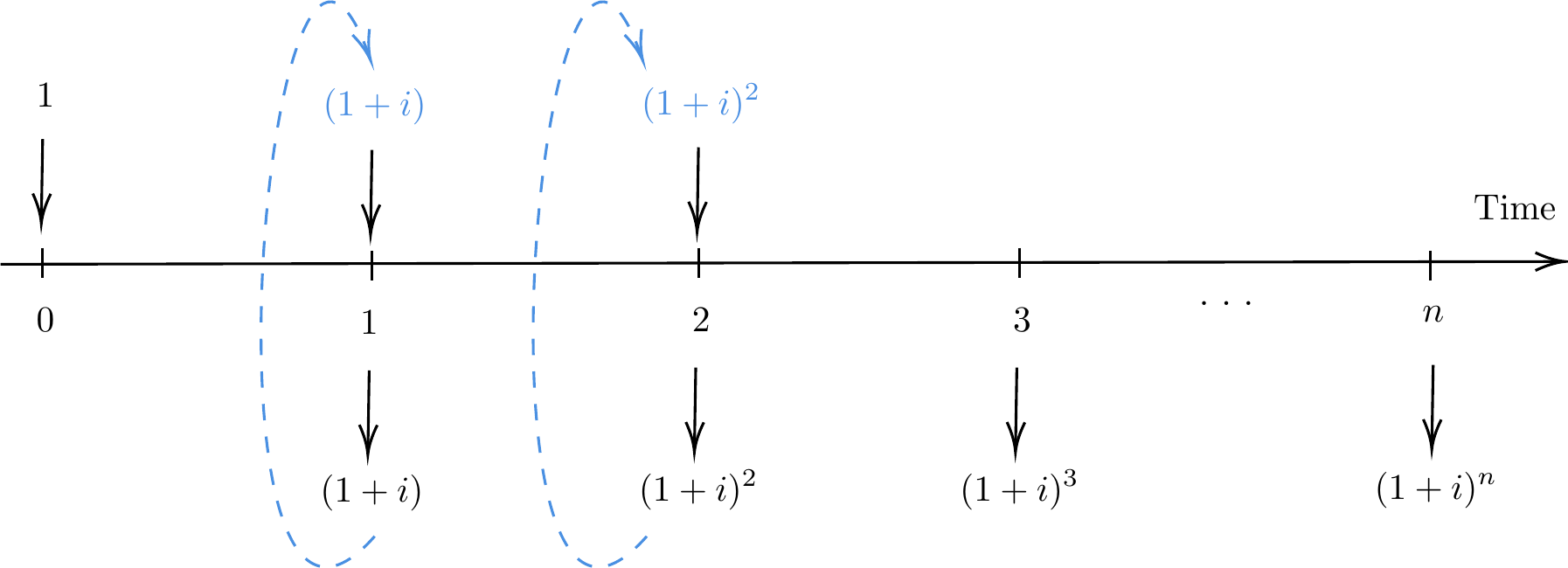
Fig. 10 a timeline of compounding interest

Example 3.9

(Excel) Use Excel to create a table showing the accumulated amounts at the end of each year for 15 years for a principal of ฿100 under the simple interest approach and the compound interest approach with \(r = 6\%\) for both cases. Discuss the results obtained (How long does it take to double the investment? How much will the principal grow over a 15-year period?)

Frequency of Compounding

Even though the interest rate is typically expressed in annual terms, an investment’s interest is frequently paid more frequently than once per year. For example, a savings account may offer an interest rate of 4% per year, credited quarterly. This interest rate is usually referred to as nominal rate of interest, i.e., 4% due four times per year.

Definition of Nominal Rate of Interest

The nominal rate of interest, also known as the stated rate or annual percentage rate (APR), is the interest rate stated in a loan agreement or investment contract. It represents the rate at which interest is applied to the principal amount annually, without considering the effect of compounding or other factors. The nominal rate of interest is typically expressed as a percentage per annum.

We will see that the frequency of interest payments, also known as the frequency of compounding, has a significant impact on the total amount accrued and the interest collected. Consequently, it is crucial to precisely specify the rate of interest.

Notation of Nominal Rate of Interest

We use \(i^{(m)}\) to represent the nominal rate of interest payable \(m\) times a year in order to underline the significance of the frequency of compounding. Therefore, \(m\) is the frequency of compounding per year and \(1/m\) year is the compounding period or conversion period.

Note The nominal rate of interest payable \(m\) times per period is also known as the rate of interest convertible \(m\)thly or compounded \(m\)thly.

Example 3.10

Calculate the accumulated value in 1 year of a deposit of ฿100 in a saving account that earns interest at 10% payable quarterly.

Solution to Example 3.10

Click to toggle answer

In this example, the nominal rate of interest of \(i^{(4)} = 10\%\) p.a. convertible quarterly means an interest rate of 10%/4 = 2.5% per quarter. In this case, the interest rate of 2.5% is the effective interest.

The effective interest rate of \(i\) per unit of time (which may be month, quarter, etc.) is the amount of interest received at the end of a unit of time per ฿1 invested at the beginning of that unit.

Therefore, the nominal interest rate \(i^{(4)} = 10\%\) is equivalent to an effective interest rate of \(2.5\%\) per quarter. The accumulated value in 1 year is

\[100 (1 + \frac{10\%}{4})^4 = 100 (1 + 2.5\%)^4 = 110.3813.\]

Note that after compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 10.3813 (or 10.3813%.p.a. effective)

Definition of Effective Rate of Interest

The effective interest rate of \(i\) per unit of time (which may be month, quarter, etc.) is the amount of interest received at the end of a unit of time per ฿1 invested at the beginning of that unit

The effective rate of interest, also known as the annual equivalent rate (AER) or annual percentage yield (APY), takes into account the effect of compounding on the nominal rate of interest. It represents the actual rate of return or cost of borrowing over a specific period, considering the compounding frequency.

The effective rate of interest provides a more accurate measure of the true cost or return on an investment or loan compared to the nominal rate, especially when interest is compounded more frequently than annually.

Example 3.11

At a rate of 12% p.a. effective, draw a timeline to show cashflows if ฿100 is invested at the start of the year.

Solution to Example 3.11

Click to toggle answer

The accumulated value of ฿100 at the end of the year is \(100 (1 + 12\%) = 112\).

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Parameters
investment = 100
interest_rate = 0.12
years = 1

# Compute future value
future_value = investment * (1 + interest_rate)

# Plotting
plt.figure(figsize=(8, 1.5))  # Adjusted height to 2 cm
plt.plot([0], [investment], marker='o', linestyle='', color='b')  # Adjusted x and y data
plt.arrow(0, investment, 0, -investment * 0.9, head_width=0.02, head_length=investment * 0.1, fc='blue', ec='blue')
plt.text(0, investment + 5, f'+{investment}', verticalalignment='bottom', horizontalalignment='center')  # Adjusted y-coordinate
plt.xlabel('Years')
plt.ylabel('Cash Flow ($)')
plt.title('Timeline of Example 3.11', y=1.3)  # Adding small space above the figure
plt.xticks(np.arange(0, years + 1, 1))  # Adjusted x ticks
plt.grid(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().get_yaxis().set_visible(False)
plt.text(0.5, investment + 5, 'i = 0.12 per year', verticalalignment='bottom', horizontalalignment='center')  # Text at x=0.5
plt.text(1, investment + 5, f'$FV = {future_value:.2f}$', verticalalignment='bottom', horizontalalignment='left')  # Adjusted x-coordinate
plt.show()

Example 3.12

At a rate of 12% p.a. compounding quarterly, draw a time line to show cashflows if ฿100 is invested at the start of the year.

Solution to Example 3.12

Click to toggle answer

The nominal interest rate \(i^{(4)} = 12\%\) is equivalent to an effective interest rate of \(3\%\) per quarter. The accumulated value in 1 year is \(100 (1 + 3\%)^4 = 112.55\). After compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 12.55 (or 12.55%. p.a. effective)

Tip

Note \(i^{(m)}\) is a nominal rate of interest which is equivalent to \(i^{(m)}/m\) applied for each \(m\)th of a period. The interest is paid \(m\) times per measurement period.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Parameters
investment = 100
interest_rate_annual = 0.12
compounding_periods_per_year = 4
years = 1

# Compute future value
interest_rate_quarterly = interest_rate_annual / compounding_periods_per_year
future_value = investment * (1 + interest_rate_quarterly)**(compounding_periods_per_year * years)

# Plotting
plt.figure(figsize=(8, 1.5))  # Adjusted height to 2 cm
plt.plot([0], [investment], marker='o', linestyle='', color='b')  # Adjusted x and y data

# Adding the arrow


plt.arrow(0, investment, 0, -investment * 0.9, head_width=0.02, head_length=investment * 0.1, fc='blue', ec='blue')

plt.text(0, investment + 5, f'+{investment}', verticalalignment='bottom', horizontalalignment='center')  # Adjusted y-coordinate
plt.xlabel('Years')
plt.ylabel('Cash Flow ($)')
plt.title('Timeline of Example 3.12', y=1.3)  # Adding small space above the figure
plt.xticks(np.arange(0, years + 1/4, 1/4))  # Adjusted x ticks
plt.grid(False)
plt.gca().spines['top'].set_visible(False)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().get_yaxis().set_visible(False)
plt.text(0.5, investment + 5, 'i = 0.03 per quarter', verticalalignment='bottom', horizontalalignment='center')  # Text at x=0.5
plt.text(1, investment + 5, f'$FV = {future_value:.2f}$', verticalalignment='bottom', horizontalalignment='left')  # Adjusted x-coordinate
plt.show()

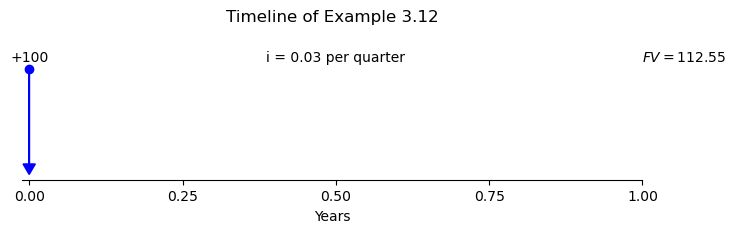
Relationship between the nominal rate and the effective rate

The relationship between the nominal rate and the effective rate is influenced by the frequency of compounding. The effective rate takes into account how often the interest is compounded within a given period, whereas the nominal rate does not consider compounding.

Tip

The following formula can be used to convert between the effective rate \(i\) p.a. and the nominal rate \(i^{(m)}\) p.a.:

\[( 1 + i) = \left( 1 + \frac{i^{(m)}}{m}\right)^m.\]

Example 3.13

Consider the following problems.

1. Express a nominal annual interest rate of 9% convertible half-yearly as a monthly effective interest.

2. Express a two-monthly effective interest of 3% as a nominal annual interest rate convertible two-monthly.

Solution to Example 3.13

Click to toggle answer

1. The effective rate \(i\)% p.a. is

\[i = ( 1 + \frac{0.09}{2})^2 - 1.\]

Hence the monthly effective rate is

\[j = (1 + i)^{1/12} - 1 = ( 1 + \frac{0.09}{2})^{2/12} - 1 = 0.007363.\]

2. A nominal annual interest rate convertible two-monthly is

\[6 \cdot 3\% = 18\%.\]

Example 3.14

Express each of the following effective rates per annum as a nominal rate, and vice versa.

Effective Rate	Nominal Rate
\(i\) = 0.04	\(i^{(4)} = 0.039412\)
\(i\) = 0.10	\(i^{(12)} = 0.095690\)
\(i\) = 0.06152	\(i^{(2)} = 0.06\)
\(i\) = 0.126825	\(i^{(12)} = 0.12\)

Compounding over any number of time units

Suppose an amount ฿1 is invested at the rate of \(i\)% per time unit. At time \(t\) the accumulation is \((1 + i)^t\).

Example 3.15

1. An investor invests ฿4000 at \(8.5\)% per quarter effective. What will be the deposit have accumulated to after 1 month.

2. An investor invests ฿800 at \(6\)% per half-year effective. What will be the deposit have accumulated to after 2.6 years.

Solution to Example 3.15

Click to toggle answer

1. The accumulation after 1 month is \(4000 \cdot 1.085^{1/3} = 4110.265768.\)

2. The accumulation after 2.6 years is \(800 \cdot 1.06^{5.2} = 1083.129754.\)

Example 3.16

(Excel) Use Excel to create a table showing the accumulated amounts after 1 year under several different compounding frequencies (yearly, quarterly, monthly, daily) for a principal of ฿100 under with nominal rate of \(r = 4\%\) per annum.

Discuss the results obtained. What happens if the compounding is made over infinitely small intervals (i.e. as \(m \rightarrow \infty\))?

Changing the time period of the effective rates of interest

It is often very useful to change the effective rate of interest per time period to another.

For example, if the effective rate of interest is defined per annum but cashflows occur monthly.

Let \(i\) be the effective rate of interest per \(t_i\) years (which can be any positive number, for e.g. \(t_i = 1/2\)). Here \(t_i\) years can be regarded as one time unit. Let \(j\) be the effective rate of interest per \(t_j\) years.

The condition under which the two effective rates of interest \(i\) and \(j\) are equivalent.

Suppose we invest 1 for one year. Then at the end of the year under each rate of interest, we will have

\[(1+i)^{1/t_i} \text{ and } (1+j)^{1/t_j}.\]

Two rates of interest are equivalent if the given amount of principal invested for the same length of time produces the same accumulated value, i.e.

\[(1+i)^{1/t_i} = (1+j)^{1/t_j}.\]

Solving the equation for \(j\) yields

\[j = (1+i)^{t_j/t_i} - 1.\]

Example 3.17

1. If the effective rate of interest is 6% per annum, what is the effective rate of interest per half-year?

2. If the effective rate of interest is 12% per two-years effective, what is the effective rate of interest per quarter-year?

3. If the effective rate of interest is 2% per month effective, what is the effective rate of interest per 1.5-years?

Solution to Example 3.17

Click to toggle answer

1. \(i = 6\%\) p.a. Then

\[j = (1.06)^{1/2} -1 = 0.029563 \text{ per half-year}.\]

2. \(i = 12\%\) per two-years. Then

\[j = (1.12)^{1/(2\times4)} -1 = 0.0142669 \text{ per quarter-year}.\]

3. \(i = 2\%\) per month. Then

\[j = (1.02)^{1.5/(1/12)} -1 = 0.428246 \text{ per 1.5-years}.\]

Non-constant interest rates

The effective rate may not be the same during every time period. We shall assume that the rates in every future time periods are known in advance.

Example 3.18

The effective rate of interest per annum was 4% during 2015, 4.5% during 2016 and 5% during 2017. Calculate the accumulation of ฿200 invested on

1. 01/01/2015 for 3 years

2. 01/07/2015 for 2 years

3. 01/04/2016 for 1.5 years

Solution to Example 3.18

Click to toggle answer

1. Accumulating the ฿200 for the first year at the rate of 4% p.a. gives

\[200 \cdot 1.04.\]

The accumulated value was then invested at the rate of 4.5% p.a. for another year, and its value at after 2 years was $\(200 \cdot 1.04 \cdot 1.045.\)$ At the rate of 5% in the final year, the value after 3 years was

\[200 \cdot 1.04 \cdot 1.045 \cdot 1.05 = 228.228.\]

2. The accumulation is

   \[200 \cdot 1.04^{1/2} \cdot 1.045 \cdot 1.05^{1/2} = 218.4025.\]

3. The accumulation is

   \[200 \cdot 1.045^{9/12} \cdot 1.05^{3/4} = 214.416986.\]

Present Value and Future Value

Definition of Present Value and Future Value

Present Value (PV) is the current worth of a future sum of money, discounted at the effective rate of interest. It represents the amount required to invest today to accumulate to a desired future value.

Future Value (FV) is the value of an investment or asset at a specified future date, compounded at the effective rate of interest. It represents the accumulation of the initial investment or principal, along with any interest or returns earned over time.

Why calculate Present Value (PV)?

• PV is calculated to evaluate the attractiveness of an investment or a financial decision by comparing the present value of expected future cash flows to the initial investment or cost.

• It helps in assessing the feasibility of projects or investments by considering the time value of money.

• PV assists in determining the fair price of financial assets, such as bonds or stocks, by discounting their future cash flows to their present value.

Why calculate Future Value (FV)?

• FV helps individuals and businesses estimate the growth potential of investments over time.

• It assists in setting financial goals and planning for long-term objectives, such as retirement savings or education funds.

• FV enables investors to compare different investment options by projecting their potential future returns.

Example 3.19: Present Value Example

Suppose you want to accumulate $1,000 in 5 years, and you have the option to invest today in a savings account that offers an effective annual interest rate of 5%. You want to calculate the present value, which represents the amount you need to invest today to achieve the desired future value.

Using the present value formula:

\[PV = \frac{FV}{(1 + r)^n}\]

Where:

• \(PV\) = Present Value

• \(FV\) = Future Value ($1,000 in this case)

• \(r\) = Effective rate of interest per period (5% in this case)

• \(n\) = Number of periods (5 years in this case)

Substituting the values:

\[PV = \frac{1,000}{(1 + 0.05)^5}\]

(1)\[PV ≈ \frac{1,000}{1.27628} ≈ 783.53\]

Interpretation: The present value of investing approximately $783.53 today, with an effective annual interest rate of 5% compounded annually, is required to accumulate to $1,000 in 5 years.

Example 3.20: Future Value Example

Suppose you invest $500 in a savings account that offers an effective annual interest rate of 8%, compounded annually. You want to calculate the future value of this investment after 3 years.

Using the future value formula:

\[FV = PV \times (1 + r)^n\]

Where:

• \(FV\) = Future Value

• \(PV\) = Present Value ($500 in this case)

• \(r\) = Effective rate of interest per period (8% in this case)

• \(n\) = Number of periods (3 years in this case)

Substituting the values:

\[FV = 500 \times (1 + 0.08)^3\]

\[FV ≈ 500 \times 1.259712 ≈ 629.86\]

(rounded to two decimal places)

Interpretation: The future value of investing $500 today, with an effective annual interest rate of 8% compounded annually, will be approximately $629.86 after 3 years.