Chapter 3 Processes for stock prices

In this chapter, we will consider some models (or processes) that are used to model stock price. The prices of stocks are continuous in time and value, which are unpredictable. However, we assume that stock prices follow a type of models (which are stochastic processes) known as geometric Brownian motion. This is one of the main tools in mathematical financial used in an analysis of derivatives. You will study in more details in the course “SCMA 459 Investment Science II”.

We will first begin with the brief introduction of the force of interest (or continuous compounding). The process for a stock price and an algorithm to simulate stock prices will be presented after main concepts of random walks and Brownian motion are given.

3.1 Force of interest

Given an annual effective rate $i$, a principal of 1 accumulates to $(1 + i)$ at the end of the first year. The following formula provides the equivalent nominal rates, $i^{(n)}$, of interest convertible $n$ times per year, \[\left(1 + \frac{i^{(n)}}{n} \right)^n = (1 + i),\] which gives \[i^{(n)} = n\left( (1+ i)^{1/n} - 1 \right).\] Note that $\displaystyle{\frac{i^{(n)}}{n}}$ is the effect interest rate applied for each $n$-th of a year. For e.g. if $n =2$, then $\displaystyle{\frac{i^{(2)}}{2}}$ is the half-yearly effect interest rate equivalent to $i$.

Example 3.1 Given the annual effective rate $i = 4\%$,

calculate the equivalent nominal rates of interest convertible $n$ times a year for $n = 2,4,12, 52,$ and 365,
find the limit of $i^{(n)}$ as $n$ tends to infinity, and
plot the graph of $i^{(n)}$ as a function of $n$.

Notes

Using the result from calculus, we can show that \[\lim_{n \rightarrow \infty} \left(1 + \frac{x}{n} \right)^n = \exp(x).\]
As $n$ tends to infinity, a rate of $i^{(n)}$ compounding $n$ times a year converges to a constant, which will be denoted by $\delta$, i.e. $i^{(n)} \rightarrow \delta$ as $n \rightarrow \infty$.
The above observations imply following relation: \[\lim_{n \rightarrow \infty} \left(1 + \frac{i^{(n)}}{n} \right)^n = \exp(i^{(\infty)}) = \exp(\delta),\] where we write $i^{(\infty)} = \delta$.
The constant $\delta$ is known as the force of interest or also known as a continuous compounded rate. It is the interest rate paid continuously throughout the period. It is a constant force that causes the initial investment to grow.
The following relationship between the force of interest and the annual effective rate of interest holds: \[1 + i = \exp(\delta) \quad \text { or } \delta = \ln(1+i).\]

Example 3.2 ฿200 is invested in an account which pays a force of interest of 4% pa. Calculate the amount in the account after 3 years.

Example 3.3 A payment of ฿500 is due in 5 years’ time. Calculate the present value of this payment at a force of interest of 4% pa.

For a force of interest $\delta$, the accumulation at time $t$ of 1 unit paid at time $s$ is \[A(s,t) = \exp( \delta (t-s)).\] The present value at time $s$ of 1 unit paid at time $t$ is \[V(s,t) = \exp( -\delta (t-s)).\] Notes

In general, the force of interest $\delta(t)$ per annum at time $t$ is a function of $t$.
Given the force of interest per annum $\delta(t)$, the accumulation at time $t$ of 1 unit paid at time $s$ is \[A(s,t) = \exp\left( \int_{s}^t \delta(s) \, ds \right).\]

Also, the present value at time $s$ of 1 unit paid at time $t$ is \[V(s,t) = \exp\left(- \int_{s}^t \delta(s) \, ds \right).\]
The more detailed discussion regarding the force of interest and continuous cashflows will be given in the course SCMA 361 Theory of Interest.

The diagram below shows the accumulation at time $t$ of 1 unit paid at time $s$ at the annual effective rate $i$ and the force of interest $\delta(t)$.

Example 3.4 A payment of ฿1000 is due in 1 years’ time. Calculate the accumulated amount at time 1 of this payment at a force of interest of $\delta(t)$ pa, where \[\delta(t) = a + b t + c t^2,\] $a,b$ and $c$ are given constants.

3.2 Stochastic processes

It is of great interest to model the behaviour of a system by describing how different states, describe by random variables $X$’s, in the system evolve with time.

Stochastic processes can be used to represent many different phenomena from various areas including science, engineering, finance, and economics. As opposed to a deterministic model whose outcome is fixed, the outcome of a stochastic process is not certain, the stochastic process is simply a collection of random variables defined as follows:

A stochastic process is a collection of random variables $\{ X_t : t \in T\}$, where

$t$ is a parameter running over some index set $T$, called the time domain.
The common sample space of the random variables (the range of possible values for $X_t$) denoted by $S$ is called the state space of the process.

Notes

The set of random variables may be dependent or need not be identically distributed.
Techniques used to study stochastic processes depend on whether the state space or the index set (the time domain) are discrete or continuous.
Topics on stochastic processes will be discussed in the course “SCMA 469 Actuarial Statistics”.

3.2.1 A simple random walk

Consider a simple model of the price of a stock measured in units of Thai baht. For each trading day $n = 0,1,2, \ldots$, the stock price increases by 1 baht with probability $p$ or decreases by 1 baht with probability $q = 1-p$.

Let $X_n$ denote the stock price at day $n$ and $X_0 =$ ฿100. This simple model is called a simple random walk.

In general, a simple random walk $X_n$ is a discrete-time stochastic process defined by

$X_0 = a$ and
for $n \ge1$, \[X_n = a + \sum_{i=1}^n Z_i, \text{ where } Z_i = \begin{cases} 1, & \text{ with probability } p \\ -1, & \text{ with probability } q = 1- p. \end{cases}\]

Note When $p = 1/2$, the value of the process increases or decreases randomly by 1 unit with equal probability. In this case, the process is known as a symmetric random walk.

Example 3.5 Calculate the expectation and variance of the random variable $Z_i$.

Solution: \[\begin{aligned} \mu &= \mathrm{E}[Z_i] = 1\cdot p + (-1) \cdot q = p - q.\\\end{aligned}\] \[\begin{aligned} \sigma^2 &= \mathrm{Var}[Z_i] \\ &=\mathrm{E}[Z_i^2] - (\mathrm{E}[Z_i] )^2 \\ &= 1 - (p-q)^2 = (p+q)^2 - (p-q)^2\\ &= 4pq.\end{aligned}\]

Example 3.6 Calculate the expectation and variance of the process $X_n$ at time $n$.

Solution: \[\begin{aligned} \mathrm{E}[X_n] &= \mathrm{E}[a + \sum_{i=1}^n Z_i] = a + n\mu.\end{aligned}\] \[\begin{aligned} \mathrm{Var}[X_n]&= \mathrm{Var}[a + \sum_{i=1}^n Z_i] = n \sigma^2.\end{aligned}\] It should be noted that the variance of $X_n$ increases with time.

The next example shows how to use a coin to simulate price paths of a stock.

Example 3.7 We flip the coin once to represent each trading day. If the coin comes up head then the stock price goes up by 1 baht; if it comes up tail then the stock price goes down by 1 baht. Assume that the initial stock price is $X_0 = 100$. Let us flip the coin 20 times and then draw the graph of the stock price against time (in day). Repeat this process 4 more times.

Solution: See the Excel worksheet.

3.2.2 Sample paths

In the simple random walk process, time is discrete (as observed at the end of each day) and the state space is discrete. The stochastic model has an infinite number of stochastic realisations. A sample path is then just the sequence of a particular set of experiments. Graphs of some stochastic realisations of the simple random walk with $p = 0.5$ and $a = 100$ are shown in Figure are shown in Figure 3.1.

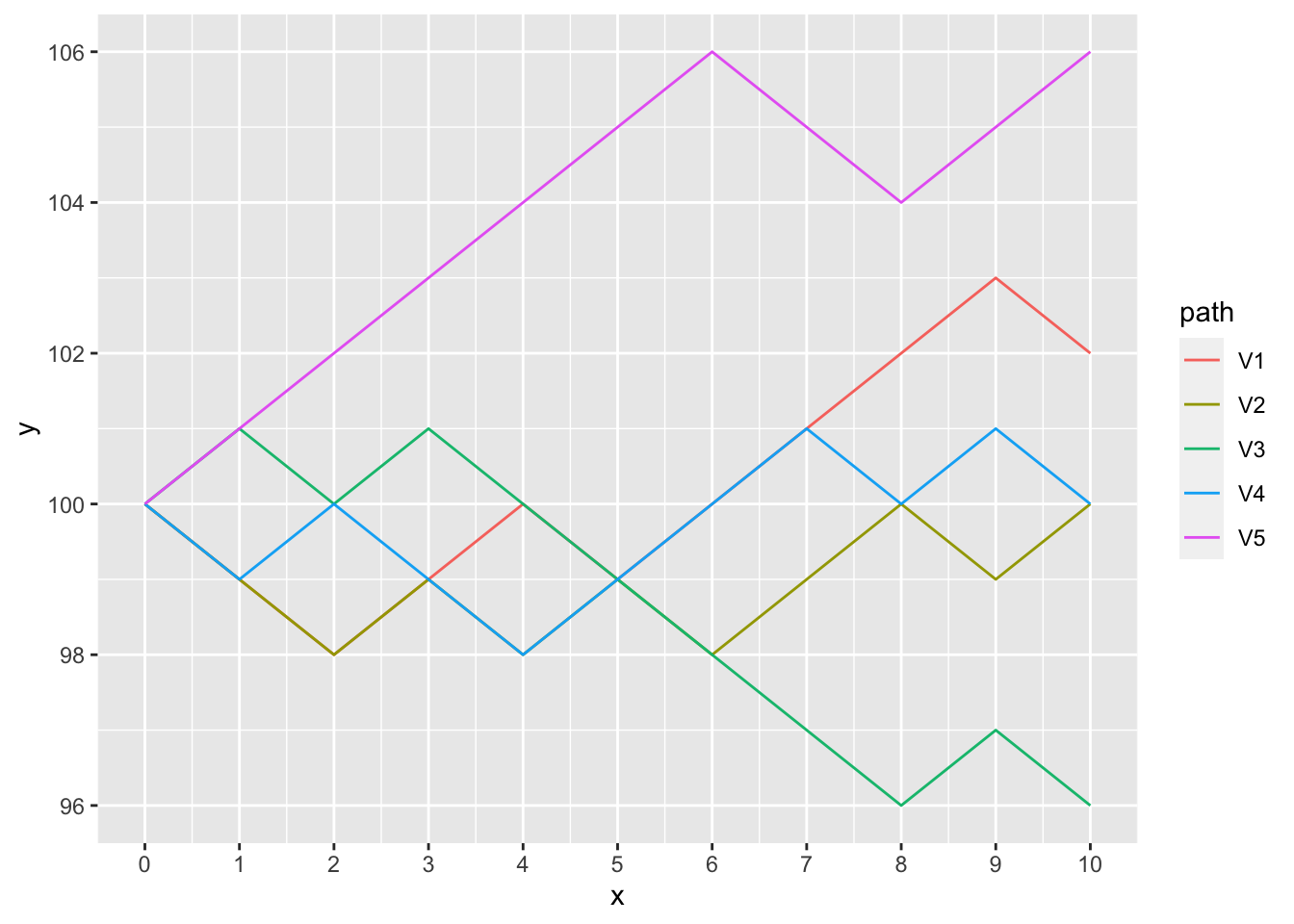
Figure 3.1: Some stochastic realisations of the simple random walk

Example 3.8 For the random process, calculate \[\Pr(X_2 = 98, X_5 = 99 | X_0 = 100).\]

Solution: The process $X_n$ must decrease on the first two days, which happens with probability $(1-p)^2$. Independently, it must then increases on another two days and decrease on one day (not necessarily in that order), giving three different possibilities. Each of these has probability $p^2(1-p)$. So \[\Pr(X_2 = 98, X_5 = 99 | X_0 = 100) = (1-p)^2 \cdot 3 p^2(1-p) = 3p^2(1-p)^3.\]

Three possible sample paths

3.2.3 Simulating a simple random walk

To simulate a sample path of the simple random walk process $X_n$ for $n = 0,1, \ldots, N$, we proceed as follows:

Generate $N$ random samples from the discrete distribution of the random variable $Z_i$, $i = 1,\ldots, N$, as follows:
1. We first generate random numbers from the uniform distribution $U(0,1)$. Denote these numbers by $U_i$.
2. If $U_i \le p$, then set $Z_i = 1$. Otherwise, $Z_i = -1$
The value $X_n$ of the random walk process at time $n$, $1 \le n \le N$, can then be calculated from \[X_n = a + \sum_{i=1}^n Z_i.\]

Notes

Excel provides two function RAND() and RANDBETWEEN(a,b) to generate a random number between 0 and 1 and a random integer between $a$ and $b$.
Excel also provides Random Number Generation to draw sample numbers from some specified distributions (to be discussed in Excel Lab).

Simulating a sample path of a simple random walk

3.3 Monte Carlo Methods

Monte Carlo methods are simulation-based algorithms that rely on generating a large set of samples from a statistical model to obtain the behaviour of the model and estimate the quantities of interest. For a large sample set of a random variable representing a quantity of interest, the law of large numbers allows to approximate the expectation by the average value from the samples.

Consider repeated independent trials of a random experiment. We will need to generate a large number of samples $X_1, X_2, \ldots$ from the model. A Monte Carlo method for estimating the expectation $\mathrm{E}[ X ]$ is a numerical method based on the approximation \[\mathrm{E}[ X] \approx \frac{1}{N}\sum_{i=1}^N X_i,\] where $X_1, X_2, \ldots$ are i.i.d. with the same distribution as $X$.

While computing expectations and computing probabilities at first look like different problems, the latter can be reduced to the former: if $X$ is a random variable, we have \[\Pr(X \in A) = \mathrm{E}[\mathbbm{1}_A(X)].\]

Using this equality, we can estimate $\Pr(X \in A)$ by \[\Pr(X \in A) = \mathrm{E}[\mathbbm{1}_A(X)] = \frac{1}{N}\sum_{i=1}^N \mathbbm{1}_A(X_i).\]

Recall that the indicator function of the set $A$ is the defined as \[\mathbbm{1}_A(x) = \begin{cases*} 1 & if $x \in A $ \\ 0 & otherwise. \end{cases*}\]

Example 3.9 Using Monte Carlo estimation, approximate the expectation $\mathrm{E}[X]$ where $X \sim \mathcal{N}(0,1)$, and estimate the percent of values lie within two standard deviation of the mean of $X$

Solution: We generate samples $X_1,X_2,...,X_N$ from the model $X$ for large $N$, for example for $N = 10000$, we can use estimates such as \[\mathrm{E}[X] \approx \frac{1}{N}\sum_{i=1}^N X_i,\] and \[\mathrm{Var}[X] \approx \frac{1}{N-1}\sum_{i=1}^N (X_i - \bar{X})^2.\]

3.4 The Markov Property

A Markov process is a special type of stochastic processes with the property that the future evolution of the process depends only on its current state and not on its past history.

That is given the value of $X_t$, the values of $X_s$ for $s > t$ do not depend on the values of $X_u$ for $u < t$. This property is called the Markov property.

A Markov process is any stochastic process that satisfies the Markov property

Notes

Stock prices are usually assumed to follow a Markov process where only the current stock price is relevant for predicting future prices, and thus the past values are irrelevant
Predictions in the future is uncertain, and must be expressed in terms of probability distributions. Hence, the probability distribution of the future stock price is independent of the particular price path in the past.
Time series models are widely used in economics, business and engineering to predict the variability of a variable over time, where past values are used as the input variables for the model.

3.5 Wiener processes

We start with the Markov process that is a building block for the geometric Brownian motion. Analogously to the random walk process, it is defined in terms of some simple intermediary processes, that is the increment process $Z_i$. The Wiener process is a Markov process which will be used to model the change in the stock prices.

The Wiener process is a (continuous-time stochastic) process which can be described by a variable $W$ having the following properties:

We assume that the current value is 0 (i.e. $W(0) = 0$) and the change in its value during a year (i.e. $W(1) - W(0)$) is $N(0,1)$ where $N(m,v)$ is a probability distribution normally distributed with mean $m$ and variance $v$.

Notes The following properties of the normal distributions are useful.
1. Given $X \sim N(\mu, \sigma^2), Y = a + bX$, it follows that \[Y \sim N(a + b\cdot \mu, b^2 \sigma^2).\]
2. Given $X \sim N(\mu_X, \sigma_X^2), Y \sim N(\mu_Y, \sigma_Y^2)$ with $X, Y$ independent, it follows that \[X + Y \sim N(\mu_X + \mu_Y, \sigma_X^2 + \sigma_Y^2).\]
3. It is well known that if two i.i.d. random variables are normally distributed, their sum is also normally distributed.
  
  The converse is also true.
  
  That is, suppose $X$ and $Y$ are two i.i.d. random variables such that $X + Y$ is normal. It necessarily the case that $X$ and $Y$ are also normal.
The probability distribution of the change in the value of the variable during any time period of length $T$ is $N(0,T)$. For example,
- The change in 2 years is the sum of two normal distributions, each of which has mean of 0 and variance of 1. Solution: \[\begin{aligned} W(2) - W(0) &= (W(2) - W(1)) + (W(1) - W(0)) \\ &\sim X + Y \text{ where } X, Y \text{ are independent } N(0,1) \text{ distributions.} \\ &\sim N(0,2).\end{aligned}\]
  
  The Markov property implies that the two distributions are independent. Hence the sum of two independent normal distributions is a normal distribution where the mean is the sum of the means and the variance is the sum of the variances.
  
  The the probability distribution of the change in the value of the variable in 2 years is $N(0,2)$.
- For the change in 6 months, the variance of the change in the value of the variable during 1 year (which is 1) equals to the sum of the variance of the change in the first 6 months and the second 6 months. We also assume that the two distributions of the six-months period are the same (or identical). As a result, the the probability distribution of the change in the value of the variable during 6 months is $N(0,0.5)$.
  
  Solution: \[\begin{aligned} W(1) - W(0) &= (W(1) - W(0.5)) + (W(0.5) - W(0)) \\ &\sim U + V \text{ where } U, V \text{ are identical and independent}\end{aligned}\] Since $W(1) - W(0) \sim N(0,1)$, it follows that $U$ and $V$ are both normally distributed $N(0,0.5)$.

Example 3.10 Given that $W(0) = a$, what is the probability distribution of the value of W at 3 months, i.e. $W(0.25)$?

Solution: \[\begin{aligned} W(0.25) &= W(0) + (W(0.25) - W(0)) \\ & \sim a + N(0,0.25) \\ & \sim N(a, 0.25).\end{aligned}\] The mean and the variance of $W(0.25)$ is $a$ and 0.25, respectively.

More precisely, a standard Brownian motion or standard Wiener process over $[0,T]$ is a random variable $W(t)$ that depends continuously on $t \in [0,T]$ and satisfies the following conditions:

$W(0) = 0$ (with probability 1).
For $0 \le s < t \le T$, the change (or increment) $W(t) - W(s)$ is normally distributed with mean zero and variance $t -s$.
For $0 \le s < t < u < v \le T$, the change (or increment) $W(t) - W(s)$ and $W(v) - W(u)$ are independent.

Notes

The second condition above implies that the change $W(t) - W(s) \sim \sqrt{t-s} N(0,1)$, where $N(0,1)$ denotes a normally distributed random variable with mean zero and unit variance.
The uncertainty about the value of the standard Brownian motion measured in terms of its standard deviation increases as the square root of how far we are looking ahead, i.e. the square root of the length of the period considered.

3.5.0.1 Simulating a standard Brownian motion

Recall that the standard Brownian motion is a continuous process. We can simulate it by discretising the time domain (the interval $[0,T]$) . The algorithm can be summarised as follows:

We set $\Delta t = T/N$ for some positive inter $N$ and let $W_j$ denote $W(t_j)$ with $t_j = j \cdot \Delta t$
Condition 1 implies that $W_0 = 0$ with probability 1, and conditions 2 and 3 tells us that \[W_j = W_{j-1} + \Delta W_j, \, j = 1,2, \ldots, N,\] where each $\Delta W_j$ is an independent random variable of the form $\sqrt{\Delta t} N(0,1)$.

Note

How can I simulate values of a normal random variable?

(Excel) If you type in any cell the formula =NORM.INV(rand(),mu,sigma), you will generate a simulated value of a normal random variable having a mean mu and a standard deviation sigma (why?).
In ordinary calculus, the notation \[dx = a dt\] indicates that $\Delta x = a \Delta t$ in the limit as $\Delta t \rightarrow 0$. This means that the change in $x$ per unit of time is constant, i.e. equal to $a$.
In stochastic calculus, we use $dW$ as a Wiener increment which is the limit of $\Delta W_j$ as $\Delta t \rightarrow 0$.
We see that the Wiener process has very jagged (irregular) sample paths.

Simulating a sample path of the standard Brownian motion

In the following example, we do not assume that $W_0 = 0$ with probability 1.

Example 3.11 Consider a Wiener process denoted by $W(t)$ with $W(0) = a$ with probability 1. The time is measured in years.

What is the probability distribution of the value of the variable at the end of one year, i.e. $W(1)$?
What is the probability distribution of the value of the variable, i.e. $W(4)$? and what is the mean and the standard deviation of $W(4)$.

What is the probability distribution of the change in the value of W during 3 months, i.e. $W(0.25) - W(0) = W(0.25)$?

3.6 Generalised Wiener process (Brownian Motion with Drift)

In this section, we will consider a variant of the standard Wiener process, which is modified by introducing the drift and variance parameters. This new process is known as a generalised Wiener process or Brownian motion with drift.

More precisely, a generalised Wiener process for a variable $X$ is defined in terms of $dW$ as \[dX = a dt + b dW,\] where $a$ is a drift parameter and $b^2$ is a variance parameter.

Note The process defined above is also known as a linear stochastic differential equation.

The term $a dt$ (deterministic term) implies that $X$ has an expected drift rate of $a$ per unit of time (or the mean change per unit time). To see this, without the stochastic or random component $b dW$, the equation is simply an ordinary differential equation \[dX = a dt \quad \text{ or } \quad \frac{dX}{dt} = a.\] The solution to this equation with an initial condition $X(0) = X_0$ is \[X = X_0 + a t.\] Clearly, for each time unit the variable $X$ increases by an amount $a$.
The stochastic or random component $b dW$, measured in terms of the variance of the change in $X$, adds uncertainty, noise or variability to the path followed by $X$. The term $b^2$ is referred to as the variance rate.

The following example shows that properties of the generalised Wiener processcan be obtained from the properties of the standard Wiener process.

Example 3.12 Calculate the probability that the generalised Wiener process $X(t)$ with the drift parameter $a = 0.5$ and the variance $b^2 = 0.16$ takes the values between 3 and 4 at time $t = 4$. Assume that its initial value $X(0) = 1$.

Solution: The change of process over 4 units of time is given by \[X(t) - X(0) = 0.5 \cdot t + 0.4 \cdot (W(t) - W(0)) = 0.5 \cdot t + 0.4 \cdot W(t) .\] The required probability is \[\begin{aligned} \Pr(3 \le X(4) \le 4) &= \Pr( 3 \le X(0) + 0.5 \cdot 4 + 0.4 \cdot W(4) \le 4 )\\ &= \Pr(0 \le W(4) \le 2.5) \\ &= \Pr(0 \le 2 Z \le 2.5), \text{ where } Z \sim N(0,1) \\ &= \Pr(0 \le Z \le 1.25) = 0.3944 \end{aligned}\] Here we can use the standard normal distribution table to obtain the probability, or use the Excel function NORM.S.DIST(z, TRUE), which returns the cumulative distribution of the standard normal distribution.

Notes

The standard Wiener process has the expected drift rate of zero, $a = 0$ and unit variance rate (noise or variability) $b^2 = 1$. For the generalised Wiener process, the amount of this noise or variability is $b$ times a Wiener process. For each time unit, the Wiener increment $dW$ follows the standard normal distribution $N(0,1)$. Therefore, the variance per time unit time of the process $X$ is equal to $b^2$.
The change in the value of the process $X$ in any time interval $t$ is normal distributed with mean of $at$ and variance of $b^2 t$, i.e. for $s, t > 0$, \[X(s + t) - X(s) \sim N(at , b^2 t).\] This follows from the definition of the process: \[\begin{aligned} X(s + t) - X(s) &= \Delta X = a \Delta t + b \Delta W\\ &= a (s + t - s) + b \Delta W = a t + b (W(s + t) - w(s)) \\ &\sim at + b \cdot N(0, t) = N(at, b^2 t),\end{aligned}\] since $W(s + t) - w(s) \sim N(0,t)$.
In general, the drift and variance rates of a stochastic process may depend on both $X$ and $t$. The process is called an Itô process and can be written as \[dX = a(X,t) dt + b(X,t) dW,\] where $a$ and $b$ are functions of $X$ and $t$.

Example 3.13 Consider the cash position of a company measured in millions of Thai baht. Assume that it follows a generalised Wiener process with a drift of 10 per year and a variance rate of 400 per year. Let $X(0) = 50$.

What is the distribution of the process at the end of the first year, $X(1)$?
What is the distribution of the process at the end of 6 months, $X(1/2)$?
What is the probability that the cash position will be at least 60 million baht at the end of 6 months?

Solution:

At the end of the first year, we know that \[X(1) - X(0) \sim N(a \cdot 1, b^2 \cdot 1),\] where $a = 10$ and $b^2 = 400$. It follows that \[X(1) \sim N(X(0) + a , b^2 ) = N(60, 400).\]
Similarly, at the end of 6 months, \[X(1/2) - X(0) \sim N(a \cdot \frac{1}{2}, b^2 \cdot \frac{1}{2}),\] or \[X(1/2) \sim N(55,200).\]
The required probability is \[\begin{aligned} \Pr( X(1/2) \ge 60) &= \Pr( Z \ge \frac{60 - 55}{\sqrt{200}} )\\ &= \Pr(Z \ge 0.35) \\ &= 1 - \text{NORM.S.DIST(0.35, TRUE)} \\ &= 1 - 0.638 = 0.362. \end{aligned}\]

3.6.0.1 Simulating a generalised Wiener process

Simulating a generalised Wiener process over $[0,T]$ is similar to a standard Wiener process.

We first discretise the interval by let $\Delta t = T/N$ for some positive integer $N$ and $t_j = j \cdot \Delta t$.
Denote $X(t_j)$ by $X_j$. The value $X_j$ can be approximated by \[X_j = X_{j-1} + a \Delta t + b \Delta W_j,\] where each $\Delta W_j = W(t_j) - W(t_{j-1})$ is an independent random variable of the form $\sqrt{\Delta t} N(0,1)$.

Simulating a sample path of the generalised Wiener process with $a =0.5$ and $b = 2$.

One-Period Simple Return

Let $P_t$ be the price of an asset at time index $t$. Holding the asset for one period from date t-1 to date t would result in a simple gross return \[1 + R_t = \frac{P_t}{P_{t-1}} \text{ or } P_t = P_{t-1} (1 + R_t).\]

Continuously Compounded Return The natural logarithm of the simple gross return of an asset is called the continuously compounded return or log return \[r_t = \ln(1 + R_t) = \ln\frac{P_t}{P_{t-1}}.\]

3.7 The process for a stock price

We will discuss a simple model (or a stochastic process) for the price of a non-dividend-paying stock. The model is known as geometric Brownian motion. We will show that this stochastic model assumes or implies the following properties for stock prices.

The process is continuous in time and value.
It possesses the Markov property, i.e. future prices depend only on its the current stock price and not on its the past historical values.
The proportional return on a stock over a short time interval is normally distributed.
The price of a stock is lognormally distributed.
The continuously compounded rate of return per year for a stock is normally distributed.

Example 3.14 Explain why a generalised Wiener (GW) process is inappropriate to model a stock price.

Solution: The GW model assumes that the expected change (not the return) is independent of the stock price, which does not explain a key aspect of stock prices. The expected percentage return (not the change in stock price) required by an investor in a short period of time, $\Delta t$, should be the same regardless of the stock price.

In particular, when either the stock price is ฿100 or ฿1000, the investor would require the same expected return.

3.7.1 Model Assumptions of the Geometric Brownian Motion

The geometric Brownian motion also consists of two components:

The deterministic component: The model assumes that the expected drift rate in $S$ (the mean change in $S$ per unit of time) is proportion to the price $S$, i.e. equal to $\mu S$, for some constant parameter $\mu$. As a result, the expected increase in $S$ in a short time interval $\Delta t$ is $\mu S \Delta t$. Therefore, without uncertainty, the model can be expressed as \[\Delta S = \mu S \Delta t\] As $\Delta t \rightarrow 0,$ the model can be described by an ordinary differential equation \[\frac{dS}{dt} = \mu S,\] and the solution to this differential equation is \[S_{T} = S_0 \exp(\mu T),\] where $S_0$ and $S_T$ are the stock prices at time 0 and time $T$.

Note When there is no uncertainty, the stock price grows at a continuously compounded rate of $\mu$ per unit of time (generally per year). If the price of the stock today is $S_0$, then its price $S_T$ at time $T$ is $S_{T} = S_0 \exp(\mu T)$.
The stochastic component:

An additional assumption of the model is that the variability of the percentage return ($\Delta S/S$) in a short time period $\Delta t$ is the same regardless of the stock price. This means that the uncertainty of the percentage return when the stock price is ฿100 is the same as that when the stock price is ฿250.

This assumption adds stochastic or random component into the model.

As a result, by adding the stochastic or random component to the deterministic component, the geometric Brownian motion can be expressed as \[dS = \mu S dt + \sigma S dW\] where $W$ is a standard Brownian motion (or a Weiner process).

Notes

The geometric Brownian motion is the continuous-time version of a random walk.
The discrete-time version of the geometric Brownian motion is \[\frac{\Delta S}{S} = \mu \Delta t + \sigma \sqrt{\Delta t} \epsilon,\] where $\epsilon$ has a standard normal distribution (with zero mean and unit variance ) The parameter $\mu$ is the expected rate of return per unit of time from the stock, and $\sigma$ is the volatility of the stock price.

3.7.1.1 Proportional return on stocks are normally distributed

It follows from the definition of the the geometric Brownian motion that the proportional return on the stock over a short time interval is normally distributed with a mean $\mu \Delta t$ and variance of $\sigma^2 \Delta t$. In particular, \[\begin{aligned} \label{propReturn} \frac{\Delta S}{S} = N( \mu \Delta t , \sigma^2 \Delta t).\end{aligned}\]

Example 3.15 Consider a stock that pays no dividends, provide an expected return of 20% per annum with continuous compounding and has a volatility of 40% per annum. Assume that the current stock price is ฿20 and $\epsilon$ sampled from the standard normal distribution is 0.6.

Calculate the change of the stock price over 1 day, assuming that there are 250 trading days per year.
Calculate the stock price over 10 days if the random samples for $\epsilon$ are given in Figure 3.6.

Solution:

Given that $\mu = 0.2$ and $\sigma = 0.4$ per annum, the process of the stock price is \[\frac{dS}{S} = \mu dt + \sigma dW.\] Here $S$ is the stock price at a particular time. If $\Delta S$ is the change in the stock price in the next small interval $\Delta$t of time, then the discrete-time version of the model is \[\begin{aligned} \frac{\Delta S}{S} &= \mu \Delta t + \sigma \sqrt{\Delta t} \epsilon \\ &= 0.2 \Delta t + 0.4 \sqrt{\Delta t} \epsilon, \end{aligned}\] where $\epsilon$ has a standard normal distribution.

For a time interval of 1 day or 0.004 years, \[\frac{\Delta S}{S} = 0.2 \cdot 0.004 + 0.4 \sqrt{0.004} \epsilon.\] If the current stock price is 20 and $\epsilon = 0.6$, then \[\Delta S = 20(0.2 \cdot 0.004 + 0.4 \sqrt{0.004} 0.6) = 0.3196,\] and $S(0.004) = S(0) + \Delta S = 20.3196.$
Leave as an exercise.

Simulating a sample path of a geometric Brownian motion with $\mu =0.2$ and $\sigma = 0.4$.

Notes

The parameter $\mu$ is the annualised expected return in a short period of time. It should depend on the risk of the return from the stock, and should also depend on the level of interest rates in the market. The higher the interest rates, the higher the expected return.
The value of a (financial) derivative, for example options, is independent of $\mu$. So we do not need to concern with the estimation of $\mu$.
The parameter $\sigma$, the stock price volatility, is important to determine the value of (financial) derivatives. We will discuss how to estimate $\sigma$.
The standard deviation of the proportional change in the stock price in a small interval $\Delta t$ is $\sigma \sqrt{\Delta t}$. For a relatively long period of time $T$, it is approximately equal to $\sigma \sqrt{T}$.

As a result, the volatility $\sigma$ can be interpreted as the standard deviation of the change in the stock price in 1 year.

Stock prices are lognormally distributed

Using Itô lemma (from stochastic calculus), it follows that stock prices are lognormally distributed: \[\begin{aligned} \label{lognormal} \ln \frac{S_T}{S_0} \sim N\left((\mu - \frac{\sigma^2}{2})T,\sigma^2 T\right) \end{aligned}\] and \[\ln S_T \sim N\left(\ln S_0 + (\mu - \frac{\sigma^2}{2})T,\sigma^2 T\right)\] where $S_T$ is the stock price at time $T$ and $S_0$ is the stock price at time 0. Here $\ln S_T$ is normally distributed and hence $S_T$ has a lognormal distribution.

Note

The logarithm of a price follows a generalised Wiener process with drift rate $\mu - \sigma^2/2$ and variance rate $\sigma^2$.
The mean of the distribution for the change in logarithm of price over each time unit (i.e. log return) is not $\mu$ but $\mu - \sigma^2/2$.
Why do stock prices follow a lognormal random variable? Let $X_i$ denotes the percentage change in the stock price during day $i$. Then the stock price at day $n$ satisfies \[S_n = S_0 \cdot X_1 \cdots X_n\] or \[\ln(S_n) = \ln(S_0) + \ln(X_1) + \cdots + \ln(X_n).\] Suppose that the changes in prices on different days are (identical) independent random variables. Then the central limit theorem implies that the sum of those independent random variables will be a normal random variable. Hence, the stock prices are lognormally distributed.
Recall that if the random variable $X$ is lognormally distributed, then $Y = \ln(X)$ has a normal distribution: \[X \sim \text{Lognormal}(\mu,\sigma^2) \Longleftrightarrow \ln(X) \sim N(\mu,\sigma^2).\]

$\mathrm{E}[X] = e^{\mu + \frac{1}{2}\sigma^2}, \, \mathrm{Var}[X] = e^{2\mu + \sigma^2}\left( e^{\sigma^2 - 1} \right).$

Example 3.16 Consider a stock that pays no dividends, provide an expected return of 20% per annum with continuous compounding and has a volatility of 40% per annum. Assume that the current stock price is ฿20.

Find the probability distribution of the logarithm of the stock price $S_T$ in 3 months’ time.
Calculate the mean and the standard deviation of $\ln S_T$ in 3 months’ time.
Find the 95% confidence interval of $S_T$ in 3 months’ time.

Solution:

Given that $\mu = 0.2$, $\sigma = 0.4$ per annum and $S_0 = 20$, the probability distribution of $\ln S_T$ in 3 months’ time ($T$ = 0.25 years) is \[\begin{aligned} \ln S_T &\sim N\left(\ln S_0 + (\mu - \frac{\sigma^2}{2})T,\sigma^2 T\right) \\ &= N\left(\ln 20 + (0.2 - \frac{0.4^2}{2}) 0.25,0.4^2 \cdot 0.25\right) = N(3.026,0.04).\end{aligned}\]
It follows that for $T$ = 0.25 years, \[\mathrm{E}[\ln S_T] = 3.026, \text{ and } \text{SD}(\ln S_T) = \sqrt{0.04} = 0.2.\]
The 95% CI of $\ln S_T$ for $T$ = 0.25 years, is \[\begin{aligned} 3.026 - 1.96 \cdot 0.2 &< \ln S_T < 3.026 + 1.96 \cdot 0.2 \\ 2.634 &< \ln S_T < 3.418.\end{aligned}\] Hence, \[\begin{aligned} e^{2.634} &< S_T < e^{3.418}\\ 13.93 &< S_T < 30.51. \end{aligned}\] There is a 95% probability that the stock price in in 3 months’ time will lie between 13.93 and 30.51.

Note It should be noted that \[\begin{aligned} \mathrm{E}[S_T] &= S_0 e^{\mu T} = 20 e^{0.2 \cdot 0.25} = 21.025 \\ &\neq e^{\mathrm{E}[\ln S_T]} = 20.615. \end{aligned}\] In particular, $\ln \mathrm{E}[S_T] \neq \mathrm{E}[\ln S_T]$.

Notes

A variable that has a lognormal distribution can take any value between zero and infinity. It is not symmetrical unlike the normal distribution.
From the properties of the lognormal distribution, the expected value of the stock price is given by (exercises) \[\mathrm{E}[S_T] = S_0 \exp (\mu T)\] and the variance of $S_T$ is \[\mathrm{Var}[S_T] = S_0^2 \exp(2 \mu T) (\exp(\sigma^2 T) - 1).\]

Example 3.17 Consider a stock that pays no dividends, provide an expected return of 20% per annum with continuous compounding and has a volatility of 40% per annum. Assume that the current stock price is ฿20. Calculate the mean and the standard deviation of the stock price $S_T$ in 1 year.

Solution: The mean of $S_1$ is \[\mathrm{E}[S_1] = 20 \exp (0.2 \cdot 1) = 24.428.\] and the variance of $S_T$ is \[\mathrm{Var}[S_1] = 20^2 \exp(2 \cdot 0.2 \cdot 1) (\exp(0.4^2 \cdot 1) - 1) = 103.539.\] and \[\text{SD}(S_1) = \sqrt{ 103.539} = 10.175.\]

3.7.2 More accurate simulation : the lognormal model

Because $T$ can be any time interval, we can use the lognormal distribution of stock prices to simulate the price of a stock at time $t + \Delta t$ given its price at time $t$. This provides accurately simulated points along a typical path, regardless of the size of $\Delta t$.

The following equations can be use to simulate stock price and estimate volatility: \[\begin{aligned} \label{lognormalModel} \ln\left( \frac{S_{t+\Delta t}}{S_t} \right) = (\mu - \frac{1}{2}\sigma^2 )\Delta t + \sigma \epsilon \sqrt{\Delta t}\end{aligned}\] and \[S_{t+ \Delta t} = S_t \exp( (\mu - \frac{1}{2}\sigma^2 )\Delta t + \sigma \epsilon \sqrt{\Delta t} )\]

Note The above equations follows from the fact that the process $\ln S$ satisfies the following stochastic differential equation \[d \ln S = (\mu - \frac{1}{2}\sigma^2 ) \, dt + \sigma \, d W.\]

3.7.3 The distribution of the rate of return

The lognormal property of stock prices can be used to show that the probability distribution of the continuously compounded rate of return per year for a stock is normally distributed.

Recall that with the continuously compounded rate $\delta$ of return per year, the accumulated value at time $T$ of the stock $S_0$ at time 0 is \[S_T = S_0 \exp(\delta T),\] or \[\delta = \frac{1}{T} \ln \frac{S_T}{S_0}.\] Hence, it follows that \[\begin{aligned} \label{returnRate} \delta \sim N\left( \mu - \frac{1}{2}\sigma^2 , \frac{\sigma^2}{T} \right).\end{aligned}\]

Notes

The standard deviation of $\delta$ declines as we consider longer time intervals. This means that
- if we hold a stock for a short time, our actual return may vary significantly from the expected return,
- but the longer we holder a stock, the more likely we are to earn a return close to the expect return.
When $T = 1$, the standard deviation of the stock return equal $\sigma$. As been seen earlier, the volatility of a stock is the standard deviation of the distribution of its continuously compounded return per year.

3.7.4 The two expected returns (this section may be skipped)

As we have seen, there are two different expected returns of stocks, $\mu$ and $\mu - \sigma^2/2$.

Equation \[propReturn\] shows that the expected percentage change (or proportional change) in the stock price in a very short period of time, $\Delta t$ is $\mu \Delta t$.

Hence, $\mu$ is the expected rate of return per year for the stock for infinitesimal interval of time.
Whereas, $\mu - \sigma^2/2$ is the expected continuously compounded rate of return per year for finite intervals of time (like days or years), i.e. realised over a period of time of length $T$ (as shown in Equation \[returnRate\]).

Notes

Recall that the expected price of a stock grows at the continuously compounded rate of $\mu$ and we can write \[\mathrm{E}[S_T] = S_0 \exp(\mu T).\]
However, the expected continuously compounded rate of return per year for a stock is $\mu - \sigma^2/2$. This is not the same as the rate of return we would calculate from the expected future price of stock return. $\mu$ is not the expected continuously compounded return on the stock.
As a result, we cannot get the expected future price of the stock by growing its current price at the expected continuously compounded rate of return per year.
If two stocks have the same price today and the same $\mu$, then their expected prices at any time in the future will be the same. The stock with the higher volatility will have a lower continuously compounded expected rate of return.

3.7.5 Estimating volatility

There are many different methods to estimate the volatility of a stock. Here the method is based on a stock’s historical volatility calculated from its daily prices for a certain number of days. As we have seen, the simulations of a stock price can be simulated by using the following equation \[\ln\left( \frac{S_{t+\Delta t}}{S_t} \right) = (\mu - \frac{1}{2}\sigma^2 )\Delta t + \sigma \epsilon \sqrt{\Delta t}.\] The estimation of the volatility of the stock price can be done as follows: Let $n+1$ denote the number of observations and $\tau$ to be the length of observation time interval in years.

Given the stock price $S_i$ at end of the $i$th interval for $i = 0,1, \ldots, n$, we define \[u_i = \ln \left(\frac{S_i}{S_{i-1}} \right), \quad \text{ for } i = 0,1, \ldots, n\]
The estimates of the mean and standard deviation of the daily returns are given by \[\begin{aligned} \bar{u} &= \frac{1}{n} \sum_{i=1}^n u_i \\ s &= \sqrt{\frac{1}{n-1} \sum_{i=1}^n (u_i - \bar{u})^2 } \\ &= \sqrt{\frac{1}{n-1} \sum_{i=1}^n u_i^2 - \frac{1}{n(n-1)} \left(\sum_{i=1}^n u_i \right)^2 }\end{aligned}\]
Because we are using observations at intervals of $\tau$ measured in years, the estimate of the annualised volatility is given by \[\hat{\sigma} = \frac{s}{\sqrt{\tau}}.\] The standard error of this estimate is approximately $\hat{\sigma}/\sqrt{2n}$.

For example, if we use daily prices and assume that there are 250 trading days in a year, then the time interval is 1/250 years. To annualise the daily volatility, we have to multiply $s$ by $\sqrt{250}$.

Note It follows from \[returnRate\] that the estimated expected return $\hat{\mu}$ is given by \[\hat{\mu} = \frac{\bar{u}}{\tau} + \frac{\hat{\sigma}^2}{2} = \frac{\bar{u}}{\tau} + \frac{s^2}{2\tau} .\]

Example 3.18 Verify the calculation using the stock price historical data from the table below.

Solution: See an accompanied Excel file.

Computation of volatility