SCMA329 Practical Mathematical Financial Modeling
2023-08-08
Chapter 1 Cashflows, Interest and the Time Value of Money
1.1 Introduction to Financial Modelling
A financial model is a financial representation of a real world financial situation, which is either a mathematical or statistical model that describes the relationship among the variables of the financial problem. Here are some types of financial models.
- Financial statement model: A financial statement model is a structured representation of a company’s financial information, typically presented in a standardized format such as an Excel spreadsheet. This model includes projections of the company’s income statement, balance sheet, and cash flow statement. It helps analysts, investors, and managers understand and evaluate a company’s financial performance, growth prospects, and overall health by forecasting how various financial metrics will evolve over time based on assumptions about revenue, expenses, and other relevant factors. (see https://corporatefinanceinstitute.com/resources/knowledge/accounting/three-financial-statements/)
- Project finance models: A project finance model is like a financial plan for a specific project, like long-term infrastructure, industrial projects, and public services. It lays out all the costs involved, such as construction, equipment, and operating expenses, and also predicts the future cash flows the project will generate, like revenue from selling electricity or tolls from the highway.
For instance, if a company wants to build a wind farm, the project finance model would estimate the costs of buying and installing wind turbines, as well as the income from selling the generated electricity over several years.
The model incorporates two main elements of the project including loans and debt repayment. It can be used to assess the risk-reward of lending to or investing in a long-term project, i.e. it can be used to tell whether the project has enough cash to cover the debt in the long term. (see https://www.wallstreetprep.com/knowledge/project-finance-model-structure/)
Discounted cashflow model: It is the model to estimate the value of an investment or business based on the present value of its future cash flows. It involves forecasting the cash flows the investment is expected to generate over time and then discounting those cash flows back to their present value using a chosen discount rate. By doing so, the model accounts for the time value of money, providing insight into whether the investment is overvalued or undervalued. (see https://corporatefinanceinstitute.com/resources/templates/excel-modeling/dcf-model-template/)
Pricing models: The pricing model is a structured approach used to determine the appropriate price for a product or service. It considers various factors such as production costs, market demand, competition, and desired profit margins to arrive at a pricing strategy. The goal is to find a balance between attracting customers and generating sufficient revenue to ensure the business’s sustainability and profitability.
This chapter covers the basic concepts of calculating interest, including simple and compound interest, the frequency of compounding, the effective interest rate and the discount rate, and the present and future values of a single payment.
1.2 Cashflows
Cashflows are amounts of money which are received (or income, positive cashflows) or paid (or outgo, negative cashflows) at particular times. Those payments arise from a financial transaction, e.g
a bank account,
a loan,
an equity,
a zero-coupon bond: A bond is a fixed income instrument that represents a loan from an investor to a debtor either a government or a corporation. A zero-coupon bond is a bond that pays no interest during its life.
a fixed interest security: A fixed-income security is a debt instrument such as a bond or debenture that investors use to lend money to a company in exchange for interest payments.
an index-linked security: An index-linked bonds pay interest that is tied to an underlying index, such as the consumer price index (CPI). Index-linked bonds are issued by governments to mitigate the effects of inflation by paying a real return plus accrued inflation.
an annuity: An annuity is a series of payments made at regular intervals, such as equal monthly payments on a mortgage.
a capital project etc.
Cash received represents inflows, income or also called positive cashflows, while money spent represents outflows, outgo or negative cashflows. The net cashflow at a given point in time is the difference between expenses and income.
Example 1.1 A series of payments into and out of a bank account is given as follows:
payments into the account : ฿1000 on 1 January 2014 and ฿100 on 1 January 2016
payments out of the account : ฿200 on 1 July 2015, ฿300 on 1 July 2016, and ฿400 on 1 January 2018
In practice, cashflows can be represented by a timeline as can be illustrated in this example.
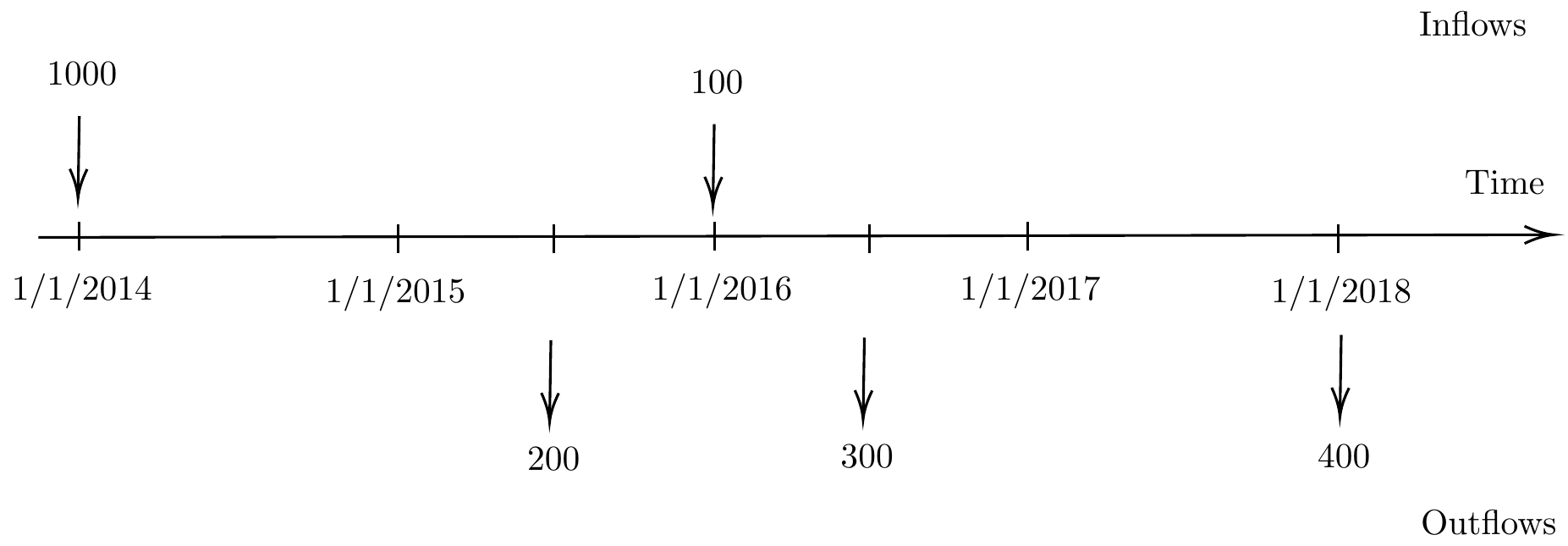
Figure 1.1: an example of a timeline
1.3 Interest and the Time Value of Money
This section introduces the time value of money using the concepts of compound interest and discounting. The effect of interest rates on the present value of future cash flows is discussed. The value of distant cash flows in the present and current cash flows in the future are then considered.
We illustrate the time value of money by considering the following examples.
Example 1.2 An investor want to make a payment of ฿10000 in 2 years. Suppose that a bank pays compound interest at 4% per annum effective. How much should the initial investment?
Note The amount we need to invest now (i.e. the initial investment in this example) is called the present value (PV) or discounted value of the payments.
Solution: The interest for year 1 is
\[ X \cdot 0.04.\] For year 2 the principal is
\[ X + X \cdot 0.04 = X \cdot (1 + 0.04)\] so that the interest for the year is
\[ X \cdot (1 + 0.04) \cdot 0.04.\]
By the end of 2 years an initial payment of ฿X will have accumulated to:
\[X\cdot (1 + 0.04) + X \cdot (1 + 0.04) \cdot 0.04 = X \cdot 1.04^2 = 10000.\] Hence,
\[X = \frac{10000}{1.04^2} = 9245.56213,\]
Note We refer to the amount to which the capital accumulates with the addition of interest as accumulation or accumulated value.
Example 1.3 Consider the following arguments
It is obvious that you would prefer to have ฿1100 now than ฿1000 now.
If we receive and hold ฿1 now, then it is worth more than receiving and holding ฿1 at some time in the future? Why is this?
Is it obvious that your would be better off with ฿1100 in 2 years than ฿1000 now?
Solution:
For the second argument, this one baht will grow to \(1 + r\) in the first year, \((1 + r)^2\) in two years, and so on. These amounts are clearly worth more than receiving and holding ฿1 at the same time in the future.
For the last argument, we need to compare the values of the amounts **received at different times. To do this, we can look at the today’s values of ฿1100 received in 2 years assuming that we can invest at an annual interest rate of \(r\) percent.
The present value of this amount \(X\) in year 2 is \[ 1100/(1 + r)^2.\] Assuming \(r = 5\%\), the present value of \(X\) is 997.7324263.
Comparing the values in today’s baths, it is better to have ฿1000 now than to have ฿1100 in 2 years.
Notes From the above example,
One can deposit or invest ฿1 now and will receive ฿1 back and a reward called interest at some point in the future. Because of its potential earning power, money in the present is worth more than an equal amount in the future. This is a fundamental financial principle known as the time value of money.
At a given point of time, cash has a monetary value, but also has a time value.
The amount deposited or invested is called capital or principal.
1.3.1 Simple interest
Simple interest is a calculation of interest that does not take into account the effect of compounding. Under simple interest, the amount of interest that accrues over time is proportional to the length of the period.
Suppose an amount \(C\) is deposited in an account that pays simple interest at the rate of \(i\)% per annum. Then after \(n\) years the deposit will have accumulated to \[C( 1 + i \cdot n).\] Hence, the interest accrued over \(n\) years is \[\text{Simple Interest} = C \cdot i \cdot n.\]
Note Auto loans and short-term personal loans are usually simple interest loans.
Example 1.4 An investor deposits ฿10000 in a bank account that pays simple interest at a rate of 5% per annum. Calculate
interest he will earn after the first two years.
interest he will earn after the first three months.
Note When \(n\) is not an integer, interest is paid on a pro-rate basis (in proportion).
Solution:
At the end of 2 years the interest earned is \[10000 \cdot 0.05 \cdot 2 = 1000.\]
At the end of 3 months the interest earned is \[10000 \cdot 0.05 \cdot \frac{3}{12} = 125.\] Alternatively, the interest per month is 5%/12 = 0.4167% and hence the interest earned can be calculated as \[10000 \cdot 0.004167 \cdot 3 = 125.\]
1.3.2 Compound interest
In compound interest, the accumulated amount over a period of time is the capital of the following period. Therefore, a capital of 1 unit at the end of the year increases to \(1 + i\) units, which becomes the capital for the following year.
For year 2, the principal is \(1 + i\) and the interest for the year is \(( 1 + i ) \cdot i\). By the end of 2 years, an initial payment of 1 will have accumuulated to \[ (1+i) + ( 1 + i ) \cdot i = (1+i)^2.\]
As this progression continues, the accumulated amount of \(X\) units at the end of year \(n\) becomes \[ X\cdot(1 + i)^n. \]
In this case, we can take money out and reinvest it as new capital illustrated in the timeline.
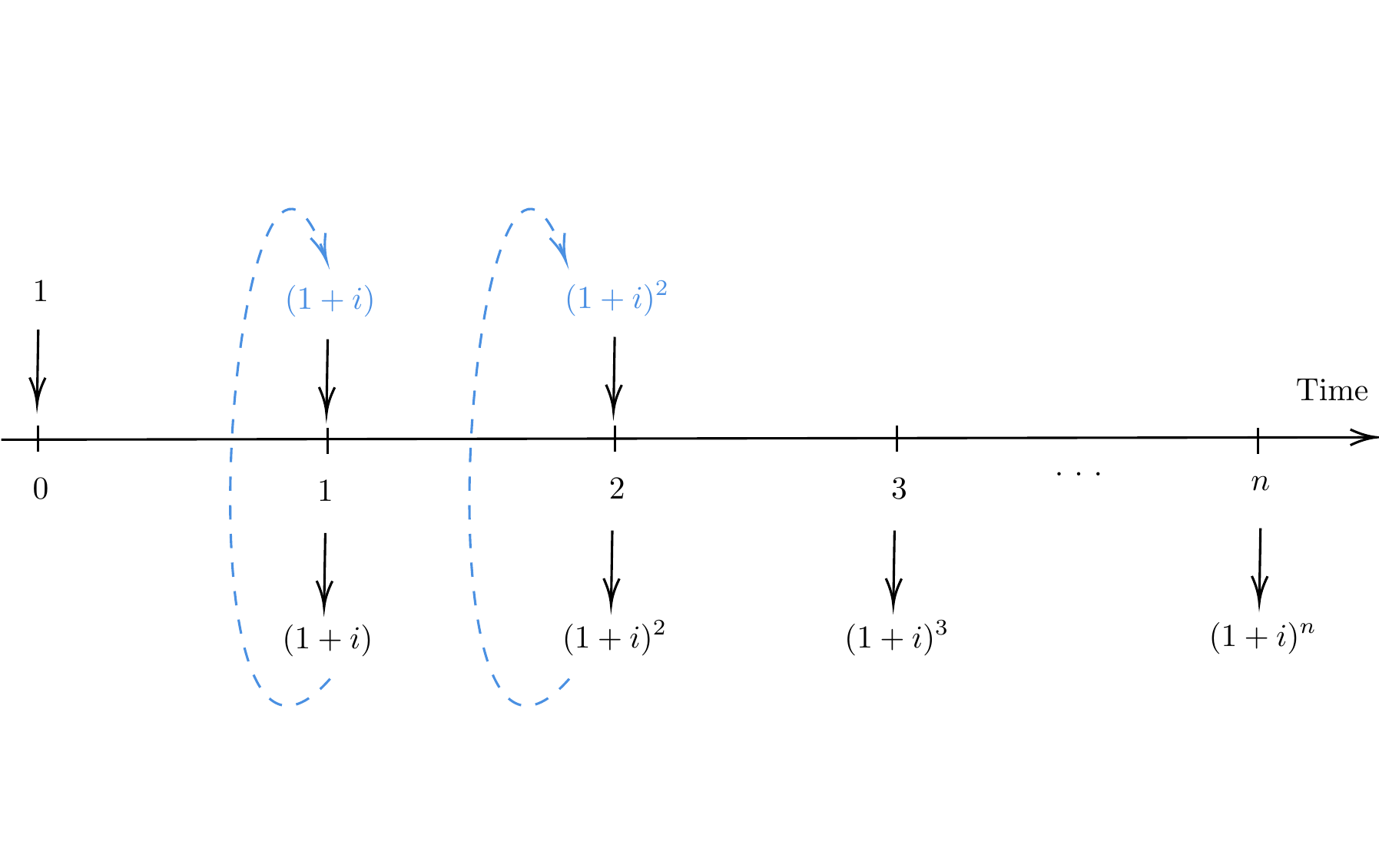
Figure 1.2: a timeline of compounding interest
Exercise 1.1 (Excel) Use Excel to create a table showing the accumulated amounts at the end of each year for 15 years for a principal of ฿100 under the simple interest approach and the compound interest approach with \(r = 6\%\) for both cases. Discuss the results obtained (How long does it take to double the investment? How much will the principal grow over a 15-year period?)
The effect of compounding is to increase the total amount of accumulation. The effect is greater when the interest rate is high. This example shows two examples of the accumulated amount of ฿100 under the simple interest approach and the compound interest approach. As can be seen, the compound interest method makes the principle increase much faster than the simple interest method when the interest rate is high.
1.4 Frequency of Compounding
Even though the interest rate is typically expressed in annual terms, an investment’s interest is frequently paid more frequently than once per year. For example, a savings account may offer an interest rate of 4% per year, credited quarterly. This interest rate is usually referred to as nominal rate of interest, i.e., 4% due four times per year.
We will see that the frequency of interest payments, also known as the frequency of compounding, has a significant impact on the total amount accrued and the interest collected. Consequently, it is crucial to precisely specify the rate of interest.
We use \(i^{(m)}\) to represent the nominal rate of interest payable \(m\) times a year in order to underline the significance of the frequency of compounding. Therefore, \(m\) is the frequency of compounding per year and \(1/m\) year is the compounding period or conversion period.
Note The nominal rate of interest payable \(m\) times per period is also known as the rate of interest convertible \(m\)thly or compounded \(m\)thly.
Example 1.5 Calculate the accumulated value in 1 year of a deposit of ฿100 in a saving account that earns interest at 10% payable quarterly.
Solution: In this example, the nominal rate of interest of \(i^{(4)} = 10\%\) p.a. convertible quarterly means an interest rate of 10%/4 = 2.5% per quarter. In this case, the interest rate of 2.5% is called effective interest. The effective interest rate of \(i\) per unit of time (which may be month, quarter, etc.) is the amount of interest received at the end of a unit of time per ฿1 invested at the beginning of that unit.
Therefore, the nominal interest rate \(i^{(4)} = 10\%\) is equivalent to an effective interest rate of \(2.5\%\) per quarter. The accumulated value in 1 year is \(100 (1 + \frac{10\%}{4})^4 = 100 (1 + 2.5\%)^4 = 110.3813\).
Note that after compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 10.3813 (or 10.3813%.p.a. effective)
Example 1.6 At a rate of 12% p.a. effective, draw a timeline to show cashflows if ฿100 is invested at the start of the year.
Solution: The accumulated value of ฿100 at the end of the year is \(100 (1 + 12\%) = 112\).
Example 1.7 At a rate of 12% p.a. compounding quarterly, draw a time line to show cashflows if ฿100 is invested at the start of the year.
Solution: The nominal interest rate \(i^{(4)} = 12\%\) is equivalent to an effective interest rate of \(3\%\) per quarter. The accumulated value in 1 year is \(100 (1 + 3\%)^4 = 112.55\). After compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 12.55 (or 12.55%. p.a. effective)
Note \(i^{(m)}\) is a nominal rate of interest which is equivalent to \(i^{(m)}/m\) applied for each \(m\)th of a period. The interest is paid \(m\) times per measurement period.
The value at time \(n\) can be considered as the annuity with a cashflow of \(i^{(m)}/m\) per period for \(n\) years together with the capital at time \(n\) as shown in the following figure. Therefore, the accumulated value in 1 year can also be calculated as \(100( 1 + 0.03 s_{\angl{4}}^{3\%})\). The concept of annuity will be discussed in the subsequent section.
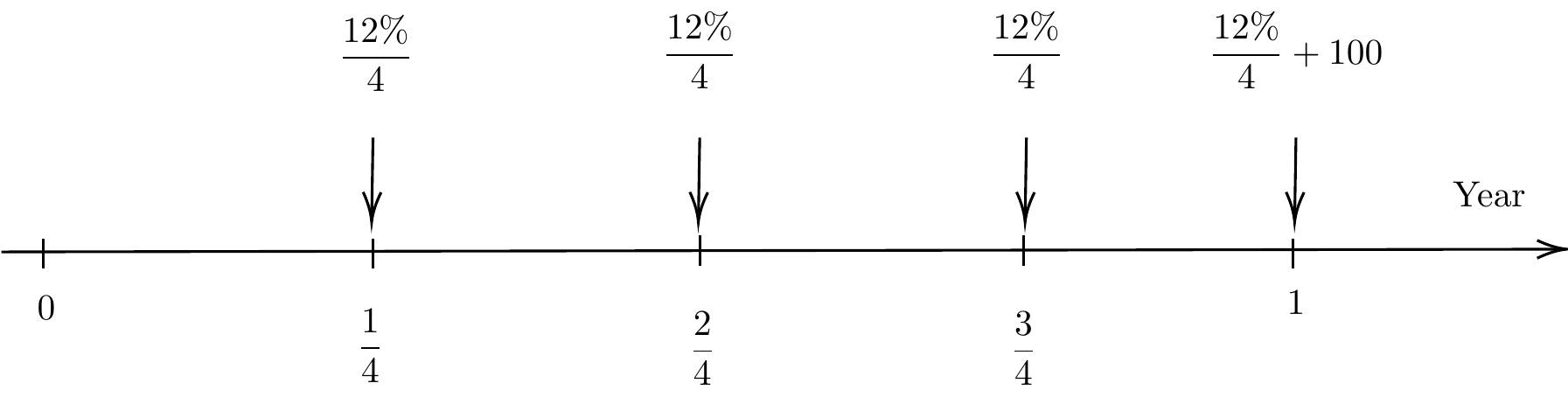
Figure 1.3: Frequency of Compouding vs Annuity
In general, we have
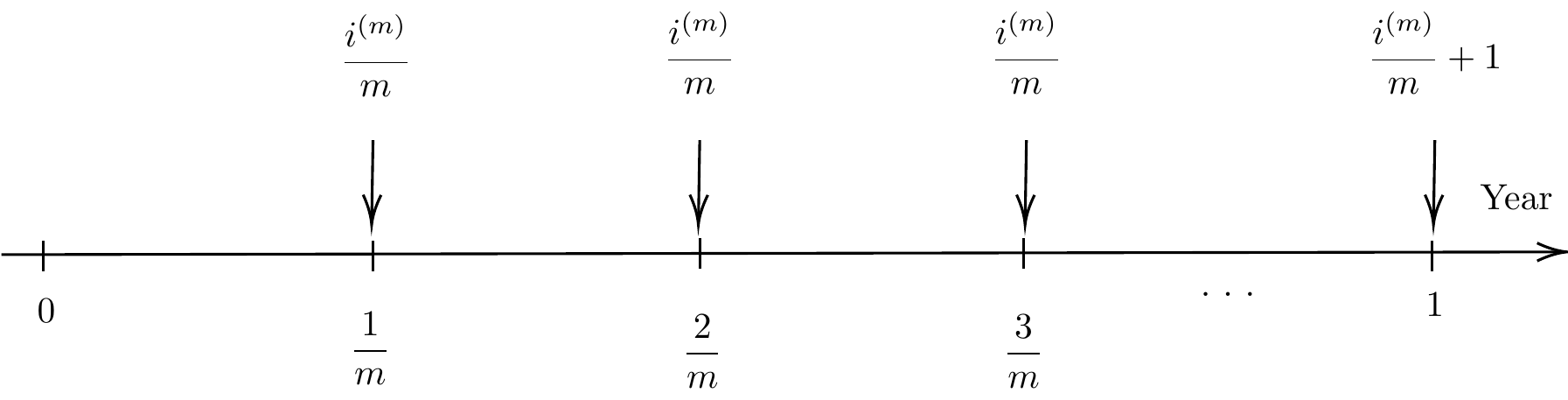
Figure 1.4: Frequency of Compouding vs Annuity
1.4.1 Effective rate of interest
The compounding frequency affects the accumulated amount. As a result, it may be inaccurate to compare two investment strategies only based on their nominal rates of return without also taking into account their frequency of compounding. It is necessary to compare different investment strategies on an equal basis. The measure known as the effective interest rate is often used for this purpose.
The effective rate of interest of \(i\) per time unit is the amount of interest received at the end of one time unit per ฿1 invested at the start of that time unit.
Example 1.8 An investor invests ฿1 at 7.5% p.a. (per annum) effective. Then \(i = 0.075\). Calculate the value of investment after one year.
Solution: The value of investment after one year at this rate is \[1 \times ( 1 + 0.075) = 1.075.\] In particular, the amount of interest received at the end of the year per ฿1 invested is 0.075.
Example 1.9 An investor invests ฿1000 at 5.25% per half-year effective. Then \(i = 0.0525\). Calculate the value of investment after half a year.
Solution: The value of investment after half year at this rate is \[1000 \times ( 1 + 0.0525) = 1052.5.\] Again, the amount ofinterest received at the end of the quarter of ฿1 invested is 0.0525.
Note The time unit is an essential part of the definition.
Example 1.10 An investor invests ฿1 at effective rate \(i\)% per time unit for \(n\) time units. Calculate the value of investment after two, three, \(\ldots\), \(n\) time units.
Note Here we assume that we can take money out and reinvest it as new capital (see the timeline).

Example 1.11 An investor invests ฿200 at \(3\)% pa effective. What will be the deposit have accumulated to after 5 years.
Solution: The deposit accumulates to \(200 \cdot (1.03)^5 = 231.854815\) after 5 years.
Example 1.12 Consider the following problems.
An investor invests ฿500 at \(2.75\)% per quarter effective. What will be the deposit have accumulated to after 9 months.
An investor invests ฿2000 at \(6\)% per half-year effective. What will be the deposit have accumulated to after 2 years.
Solution:
Accumulating the 500 for 9 months at this rate gives \[500 \cdot (1.0275)^3 = 542.394773.\]
After 2 years the accumulation is \[2000 \cdot (1.06)^4 = 2524.95392.\]
Notes
The model under the effective rate of interest condition is a model of compound interest, where interest is earned on interest previously earned. Unless state otherwise, we shall assume that \(i\) is the compound interest rate.
In practice, it is easier to work with the effective rate of interest which is defined in a suitable time unit.
The following formula can be used to convert between the effective rate \(i\) p.a. and the nominal rate \(i^{(m)}\) p.a.: \[( 1 + i) = \left( 1 + \frac{i^{(m)}}{m}\right)^m.\]
Example 1.13 Consider the following problems.
Express a nominal annual interest rate of 9% convertible half-yearly as a monthly effective interest.
Express a two-monthly effective interest of 3% as a nominal annual interest rate convertible two-monthly.
Solution:
The effective rate \(i\)% p.a. is \[i = ( 1 + \frac{0.09}{2})^2 - 1.\] Hence the monthly effective rate is \(j = (1 + i)^{1/12} - 1 = ( 1 + \frac{0.09}{2})^{2/12} - 1 = 0.007363\).
A nominal annual interest rate convertible two-monthly is \(6 \cdot 3\% = 18\%\).
Example 1.14 Express each of the following effective rates per annum as a nominal rate, and vice versa.
| Effective Rate | Nominal Rate |
|---|---|
| \(i\) = 0.04 | \(i^{(4)} = 0.039412\) |
| \(i\) = 0.10 | \(i^{(12)} = 0.095690\) |
| \(i\) = 0.06152 | \(i^{(2)} = 0.06\) |
| \(i\) = 0.126825 | \(i^{(12)} = 0.12\) |
1.4.2 Compounding over any number of time units
Suppose an amount ฿1 is invested at the rate of \(i\)% per time unit. At time \(t\) the accumulation is \((1 + i)^t\).
- Example 1.15
An investor invests ฿4000 at \(8.5\)% per quarter effective. What will be the deposit have accumulated to after 1 month.
An investor invests ฿800 at \(6\)% per half-year effective. What will be the deposit have accumulated to after 2.6 years.
Solution:
The accumulation after 1 month is \(4000 \cdot 1.085^{1/3} = 4110.265768.\)
The accumulation after 2.6 years is \(800 \cdot 1.06^{5.2} = 1083.129754.\)
Exercise 1.2 (Excel) Use Excel to create a table showing the accumulated amounts after 1 year under several different compounding frequencies (yearly, quarterly, monthly, daily) for a principal of ฿100 under with nominal rate of \(r = 4\%\) per annum.
Discuss the results obtained. What happens if the compounding is made over infinitely small intervals (i.e. as \(m \rightarrow \infty\))?
1.4.3 Changing the time period of the effective rates of interest
It is often very useful to change the effective rate of interest per time period to another. For example, if the effective rate of interest is defined per annum but cashflows occur monthly.
Let \(i\) be the effective rate of interest per \(t_i\) years (which can be any positive number, for e.g. \(t_i = 1/2\)). Here \(t_i\) years can be regarded as one time unit. Let \(j\) be the effective rate of interest per \(t_j\) years.
Example 1.16 Find the condition under which the two effective rates of interest \(i\) and \(j\) are equivalent.
Solution: Suppose we invest 1 for one year. Then at the end of the year under each rate of interest, we will have \[(1+i)^{1/t_i} \text{ and } (1+j)^{1/t_j}.\] Two rates of interest are equivalent if the given amount of principal invested for the same length of time produces the same accumulated value, i.e. \[(1+i)^{1/t_i} = (1+j)^{1/t_j}.\] Solving the equation for \(j\) yields \[j = (1+i)^{t_j/t_i} - 1.\]
- Example 1.17
If the effective rate of interest is 6% per annum, what is the effective rate of interest per half-year?
If the effective rate of interest is 12% per two-years effective, what is the effective rate of interest per quarter-year?
If the effective rate of interest is 2% per month effective, what is the effective rate of interest per 1.5-years?
Solution:
\(i = 6\%\) p.a. Then \[j = (1.06)^{1/2} -1 = 0.029563 \text{ per half-year}.\]
\(i = 12\%\) per two-years. Then \[j = (1.12)^{1/(2\times4)} -1 = 0.0142669 \text{ per quarter-year}.\]
\(i = 2\%\) per month. Then \[j = (1.02)^{1.5/(1/12)} -1 = 0.428246 \text{ per 1.5-years}.\]
1.4.4 Non-constant interest rates
The effective rate may not be the same during every time period. We shall assume that the rates in every future time periods are known in advance.
Example 1.18 The effective rate of interest per annum was 4% during 2015, 4.5% during 2016 and 5% during 2017. Calculate the accumulation of ฿200 invested on
01/01/2015 for 3 years
01/07/2015 for 2 years
01/04/2016 for 1.5 years
Solution:
Accumulating the ฿200 for the first year at the rate of 4% p.a. gives \[200 \cdot 1.04.\] The accumulated value was then invested at the rate of 4.5% p.a. for another year, and its value at after 2 years was \[200 \cdot 1.04 \cdot 1.045.\] At the rate of 5% in the final year, the value after 3 years was \[200 \cdot 1.04 \cdot 1.045 \cdot 1.05 = 228.228.\]
The accumulation is \[200 \cdot 1.04^{1/2} \cdot 1.045 \cdot 1.05^{1/2} = 218.4025.\]
The accumulation is \[200 \cdot 1.045^{9/12} \cdot 1.05^{3/4} = 214.416986.\]
1.4.5 Accumulation factors
Let \(i\) be the effective rate of interest per one time unit and \(s < t\). We define
the accumulation factor per one time unit \[A(0,1) = (1 + i).\]
the accumulation factor per \(t\) time units \[A(0,t) = (1 + i)^t.\]
the accumulation factor at time \(t\) of 1 unit invested at time \(s\) \[A(s,t).\]
Example 1.19 The effective rate of interest per annum was 6% during 2015, 8% during 2016 and 10% during 2017. Calculate the following accumulation factors.
\(A(01/01/15, 01/01/18),\) i.e. the accumulation at 01/01/18 of an investent of 1 at 01/01/15
\(A(01/07/15, 01/07/17)\)
\(A(01/04/16, 01/10/17)\)
Solution:
\(A(01/01/15, 01/01/18) = (1.06)(1.08)(1.1) = 1.25928\)
\(A(01/07/15, 01/07/17) = (1.06)^{1/2}(1.08)(1.1)^{1/2} = 1.166200\)
\(A(01/04/16, 01/10/17) = (1.08)^{3/4}(1.1)^{3/4} = 1.137922\)
1.4.6 Present values and discount factors
Recall from Example 1.2 that the amount \(\displaystyle{\frac{10000}{1.04^2}}\) we need to invest now to obtain ฿10000 in two years is called the present value (PV) or discounted value of the payments.
We define the discount factor \(v\) per annum, at rate \(i\) p.a. effective to be the present value of a payment of 1 due in 1 year?s time, i.e. \[v = \frac{1}{1+i}.\]
Example 1.20 Calculate the present of ฿25000 due in 3 years at an effective rate of interest of 6% per annum.
Solution: The present value is \[25000 \cdot \frac{1}{1.06^3} = 20990.482076.\] It is the discounted value of 25000 due in 3 years.
Example 1.21 How much should we invest now to meet a liability of ฿50000 in 5 years at an effective rate of interest of 3% per half-year.
Solution: The amount we need to invest now to meet the future liability of 50000 in 5 years is the present value \[50000 \cdot \frac{1}{1.03^{10}} = 37204.695745.\]
Note It follows that the \(PV\) of ฿1 in \(t\) time units at \(i\) effective rate of interest per time unit is \[PV = \frac{1}{(1+i)^t} = v^t.\]
Example 1.22 Given the discount factor per year \(v = 0.9\), calculate
the effective rate of interest per year.
the equivalent discount factor per half-year.
Solution:
From \(\displaystyle{ v= \frac{1}{1+i} = 0.9}\), solving the equation for \(i\) gives \[i = \frac{1}{v} - 1 = 0.111111 \text{ per year}.\]
Let \(j\) be the effective rate of interest per half-year. Then \[j = (1+ i)^{1/2} -1 = 0.054093.\] Then, the discount factor per half-year is \[v = \frac{1}{1+j} = \frac{1}{1.054093} = 0.948683.\]
Similarly, we define
the discount factor per one time unit \[V(0,1) = 1/(1 + i).\]
the discount factor per \(t\) time units \[V(0,t) = 1/(1 + i)^t.\]
for \(s < t\), the discount factor at time \(s\) of 1 unit receivable at time \(t\) \[V(s,t) = (1 + i)^{s - t}.\]
Notes
\(V(s,t) = A(s,t)^{-1}\)
For \(r < s < t\), the following holds:
\(A(r,t) = A(r,s) A(s,t)\)
\(V(r,t) = V(r,s) V(s,t)\)
1.5 Cashflows and Annuities
Consider a series of cashflows defined by (see the timeline)
the times of payments (cashflows), denoted by \(t_1, t_2, \ldots,\) and
the amount of payments, denoted by \(C_{r}\) (or \(C_{t_r}\)), which will be paid at time \(t_r\), for \(r = 1,2, \ldots\). The amounts can be positive or negative
The present value at any time \(t\) of this series of cashflow is \[PV(t) = \sum_{r=1}^\infty C_r (1 + i)^{t - t_r} = \sum_{r=1}^\infty C_r v^{t _r - t}\] where \(i\) is the effective rate of interest.
The above formula can be obtained by summing these two components:
for all \(t_r < t\), adding up the accumulations of these individual cashflows up to time \(t\), and
for all \(t_r > t\) , adding up the discounted values of these individual cashflows back to time \(t\).

Notes
At a fixed effective rate of interest, the original series of cashflows is equivalent to a single payment of amount \(PV(t)\) at time \(t\).
If two different series of cashflows have the same \(PV\) at one time at a given effective rate of interest, then they have the same \(PV\) at any time at that effective rate of interest.
Example 1.23 Let \(i = 4\%\) effective per time unit. Cashflows are given as follows:
\(C_1 = 200\) at time \(t_1 = 1\).
\(C_2 = 300\) at time \(t_2 = 3\).
\(C_3 = -100\) at time \(t_3 = 5\).
\(C_4 = -50\) at time \(t_4 = 6\).
Calculate
the accumulation at time \(t = 7\).
the present value at time \(t = 0\).
the present value at time \(t = 4\).
Solution:

The series of cashflows is shown in the following timeline. The accumulation at time \(t = 7\) is \[\begin{aligned} \sum_{r=1}^4 A(t_r,7) &= 200 \cdot A(1,7) + 300 \cdot A(3,7) - 100 \cdot A(5,7) - 50 \cdot A(6,7) \\ &= 200 \cdot 1.04^6 + 300 \cdot 1.04^4 - 100 \cdot 1.04^2 - 50 \cdot 1.04 \\ & = 443.861372\end{aligned}\]
The present value at time \(t = 0\) can be obtained by discounting the accumulation at time \(t = 7\) back to time \(t = 0\), which is \[443.861372 \cdot V(0,7) = 443.861372 \cdot \frac{1}{1.04^7} = 337.298163.\]
The present value at time \(t = 4\) is \[443.861372 \cdot V(4,7) = 443.861372 \cdot \frac{1}{1.04^3} = 394.591143.\]
1.5.1 Level Annuities certain
An annuity is a series of payments made at equal intervals. There are many practical examples of financial transactions involving annuities, such as.
a car loan that is repaid in equal monthly instalments
a pensioner who purchases an annuity from an insurance company upon retirement
a life insurance policy that is taken out with monthly premiums
When certain payments are to be made for a certain period of time, they are called annuity certain.
If the payments are made at the end of each time period, they are paid in arrears.
Otherwise, payments are made at the beginning of each time period, they are pain in advance.
An annuity paid in advance is also known as an annuity due
If each payment is for the same amount, this is a level annuity.
Example 1.24 Let \(i\) be the constant effective rate of interest per time unit. Show that the accumulated value of a level annuity certain having cashflow of 1 unit at the end of each of the next \(n\) time units is \[\frac{(1+i)^n -1 }{i}.\] Such accumulated value of the annuity is denoted by \(s_\angl{n}\) (pronounced “S.N.”)

Solution: Based on the first principles,
\[\begin{align} s_\angl{n} &= \sum_{r=1}^n C_r \cdot A(t_r,n) \\ &= (1+i)^{n-1} + (1+i)^{n-2} + \ldots + (1+i) + 1. \tag{1.1} \end{align}\]Multiplying Eq.(1.1) through by (1+i) gives \[\begin{equation} (1+i) \cdot s_\angl{n} = (1+i)^{n} + (1+i)^{n-1} + \ldots + (1+i)^2 + (1+i). \end{equation}\] Subtracting the two equations results in \[\begin{aligned} i \cdot s_\angl{n} &= (1+i)^{n} - 1\\ s_\angl{n} &= \frac{(1+i)^{n} - 1}{i}.\end{aligned}\]
Example 1.25 Let \(i\) be the constant effective rate of interest per time unit. Show that the present value at time 0 of a level annuity certain, denoted by \(a_\angl{n}\) (pronounced “A.N.”) , having cashflow of 1 unit at the end of each of the next \(n\) time units is \[a_\angl{n} = \frac{1 - v^n }{i}.\]
Solution: Taking the accumulated value at time \(n\) and discounting back to time 0 gives \[\begin{aligned} a_\angl{n} &= s_\angl{n} \cdot v^n \\ &= \frac{(1+i)^{n} - 1}{i} \cdot v^n \\ &= \frac{1 - v^n }{i}.\end{aligned}\]
Example 1.26 Given the effective rate of interest of \(8\%\) p.a., calculate
the accumulation at 12 years of ฿500 payable yearly in arrears for the next 12 years.
the present value now of ฿2,000 payable yearly in arrears for the next 6 years.
the present value now of ฿1,000 payable half-yearly in arrears for the next 12.5 years.
Solution:
- The timeline of this transaction is shown in the figure below.

The accumulation of the payments is
$$500 \cdot s_\angl{12} = 500 \cdot \frac{1.08^{12} - 1 }{0.08 } = 9488.563230.$$The present value of the payments is \[2000\cdot a_\angl{6} = 2000 \cdot \frac{1 - 1.08^{-6} }{0.08 } = 9245.759328.\]
An interest rate of 8% p.a. is equivalent to an effective half-yearly interest rate, denoted by \(j\), of \[j = 1.08^{1/2} -1 = 0.039230.\] There are 25 payments of 1000 each, starting in six months’ time.
Working in terms of half year, the present value of the payment is \[1000 \cdot a^j_\angl{25} = 1000 \cdot \frac{1 - 1.039230^{-25} }{0.039230 } = 15750.003911.\]
1.5.2 Level Annuities Due
An annuity-due is an annuity where the payments made at the start of each time period (instead of a the end), i.e. the payments are paid in advance.
In order to calculate the present value or accumulation of an annuity due, we first introduce the concept of the rate of discount.
The rate of discount
As opposed to the interest rate where the accumulation of initial investment can be obtained by multiplying it by the accumulation factor \((1+i)^n\), we can obtain the discounted value of payment by using discount rates.
Suppose an amount of ฿1 is due after 1 year with an effective rate of \(i \%\) p.a. (see the timeline below). What is the amount of money required to invested now to accumulate to 1?
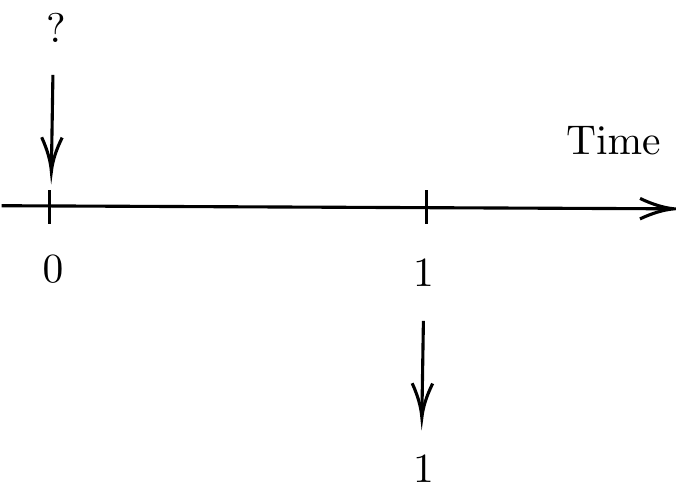
The amount of money required now to accumulate to ฿1 in one year is \[v = \frac{1}{1+i}.\] Note that \[\frac{1}{1+i} = 1 - \frac{i}{1+i}.\] We define the effective rate of discount \(d\) per annum as\[d = \frac{i}{1+i}.\] It follows that \[v = \frac{1}{1+i} = 1 - \frac{i}{1+i} = 1 - d\] represents the discount of ฿1 for 1 year using the effective rate of interest of \(i \%\) p.a.
Similarly, suppose an amount of ฿1 is due after \(n\) year with an effective rate of \(i \%\) p.a. The amount of money required to invested now to accumulate to 1 in \(n\) year is \[\frac{1}{(1+i)^n} = (1-d)^n.\] See the timeline below for illustration.

Example 1.27 Discount ฿2,000 for 3 years using the effective rate of discount of 5% per annum.
Solution: After 1 year the discount will be \(0.05 \cdot 2000 = 100,\) and the discounted value of the payment will be \[2000 \cdot (1 - d) = 2000 \cdot (1 - 0.05) = 1900 .\] Similarly, after 2 years, the discounted value will be \[2000 \cdot (1 - d)^2 = 2000 \cdot (1 - 0.05)^2 = 1805 .\] After 3 years, the discounted value of the payment will be \[2000 \cdot (1 - d)^3 = 2000 \cdot (1 - 0.05)^3 = 1714.75 .\]
Example 1.28 The effective rate of discount \(d\) per time unit can be regarded as the interest paid in advance at time 0, which is equivalent to the effective rate of interest \(i\) payable in arrears.
Solution: To show this, suppose that the bank added interest of \(x\) to an account of an amount of 1 unit at the start of the period. Assume that the interest amount of \(x\) can be withdrawn and invested in another bank that earn the rate of interest \(i\%\) effective per time unit. The principle of 1 unit is still in the first bank.

At the end of the year, we have
the principle of 1 unit in the first bank, and
the interest paid in advance which accumulates to \(x(1+i)\) in the second bank.
For this to be equivalent to the interest paid in arrears, we can find \(x\) which solves \[\begin{aligned} 1 + x(1+i) &= 1 + i,\\ x &= \frac{i}{1+i} = \frac{1+i}{1+i} - \frac{1}{1+i} = 1-v = d.\end{aligned}\] Therefore, the effective rate of discount \(d\) per time unit can be regarded as the interest paid in advance at time 0, which is equivalent to the effective rate of interest \(i\) payable in arrears.
Example 1.29 Let \(i\) be the constant effective rate of interest per time unit. Show that the accumulated value of a level annuity due, denoted by \(\ddot{s}_\angl{n}\) (pronounced “S-due N”, having cashflow of 1 unit at the start of each of the next \(n\) time units is \[\ddot{s}_\angl{n} = \frac{(1+i)^n -1 }{d}.\]

Solution: Using the previous results, it follows that \[\begin{aligned} \ddot{s}_\angl{n} &= (1+i)^n + (1+i)^{n-1} + \cdots + (1+i)^2 + (1+i) \\ &= (1+i) \cdot \left[(1+i)^{n-1} + \cdots + (1+i)^1 + 1\right] \\ &= (1+i) \cdot {s}_\angl{n} \\ &= (1+i) \cdot \frac{(1+i)^n -1 }{i}\\ &= \frac{(1+i)^n -1 }{i/(1+i)}\\ &= \frac{(1+i)^n -1 }{d}.\end{aligned}\]
Example 1.30 Let \(i\) be the constant effective rate of interest per time unit. Show that the present value at time 0 of a level annuity due having cashflow of 1 unit at the start of each of the next \(n\) time units is \[\ddot{a}_\angl{n} = \frac{1 - v^n }{d}.\]
Solution: The present values of the payments can be obtained by discounting \(\ddot{a}_\angl{n}\) back to time 0, i.e. \[\begin{aligned} \ddot{a}_\angl{n} &= v^n \cdot \ddot{s}_\angl{n} \\ &= v^n \frac{(1+i)^n -1 }{d} \\ &=\frac{1 - v^n}{d}.\end{aligned}\]
Example 1.31 Given the effective rate of interest of \(8\%\) p.a., calculate
the accumulation at 12 years of ฿500 payable yearly in advance for the next 12 years.
the present value now of ฿2,000 payable yearly in advance for the next 6 years.
the present value now of ฿1,000 payable half-yearly in advance for the next 12.5 years.
Solution:
The accumulation of the annuity-due of 12 years is \[500 \cdot \ddot{s}_\angl{12} = 500 \cdot \frac{1.08^{12} -1}{0.08/1.08} = 10247.648289.\]
The present value of the annuity-due of 6 years is \[2000 \cdot \ddot{a}_\angl{6} = 2000 \cdot \frac{1- 1.08^{-6}}{0.08/1.08} = 9985.420074.\]
An interest rate of 8% p.a. is equivalent to an effective half-yearly interest rate, denoted by \(j\), of \[j = 1.08^{1/2} -1 = 0.039230.\] There are 25 payments of 1000 each, starting in six months’ time.
Working in terms of half year, the present value of the payment is \[1000 \cdot \ddot{a}^j_\angl{25} = 1000 \cdot \frac{1 - 1.039230^{-25} }{0.039230/1.039230 } = 16367.876564.\]
1.5.3 Deferred annuities
An annuity whose first payment is made during the first time period (either in arrears or in advance) is called immediate annuity. Otherwise, the annuity is known as deferred annuity, i.e. the first payment starts some time in the future.
To calculate the present value of the annuity of a series of \(n\) payments deferred for \(m\) time units (the first payment is due at time \(m+1\)), denoted by \(_{m \textbar}a_\angl{n}\), we first calculate the present value at the end of the deferred period and then discount back to the start of the period.

\[\begin{aligned} _{m \textbar} a_\angl{n} &= v^{m+1} + v^{m+2} + \cdots +v^{m+n} \\ &= v^m \left( v + v^2 + \cdots + v^n \right) \\ &= v^m \cdot a_\angl{n}.\end{aligned}\]
Example 1.32 Calculate the present value at time 0 of an annuity of 1 p.a. in arrears for 6 years and deferred for 10 at 6% effective rate p.a.

This is an annuity with 6 unit payments for which the first payment is at time 11. Hence the present values of such payments is \[\begin{aligned} _{10 \textbar}a_\angl{6} &= v^{11} + v^{12} + \cdots +v^{16} \\ &= v^{10} \left( v + v^2 + \cdots + v^6 \right) \\ &= v^{10} \cdot a_\angl{6} \\ &= \left(\frac{1}{1.06}\right)^{10} \cdot \left( \frac{1- 1.06^{-6}}{0.06} \right) &= 2.745808.\end{aligned}\]
Example 1.33 Give the reason or show that the present value of a series of \((n+m)\) payments of one unit payable at the end of each time period is equal to the sum of
present value of \(m\) payments of one units payable at the end of each time period (denoted by \(a_\angl{m}\)) and
present value of \(n\) payments of one units payable at the end of each time period deferred for \(m\) years (denoted by \(_{m \textbar}a_\angl{n}\)).
Solution: The present value of a series of (m+n) payments is \[\begin{aligned} a_\angl{m+n} &= \left( v + v^2 + \cdots v^m\right) + \left( v^{m+1} + v^{m+2} + \cdots +v^{m+n} \right) \\ &= a_\angl{m} + _{m \textbar}a_\angl{n}.\end{aligned}\] It follows that \(_{m \textbar}a_\angl{n} = a_\angl{m+n} - a_\angl{m}.\)
1.5.4 Increasing annuities
An annuity in which the \(i\)th payment of the amount \(i\) is made at time \(t_i = i\) is called an (simple) increasing annuity. The present and accumulated value of this annuity can be obtained from the first principles. For example, the present value of the increasing annuity can be evaluated by \[\sum_{i=1}^n X_i v^{t_i} = \sum_{i=1}^n i v^{t_i},\] where the \(i\)th payment of amount \(X_i = i\) at time \(t_i = i\).
Example 1.34 Derive the formula for the present value of a simple increasing annuity payable yearly in arrears with the effective rate \(i\%\) p.a. for \(n\) years.
Solution: The cashflows of the simple increasing annuity payable yearly in arrears is illustrated below. The present value of payments of 1 at time 1, 2 at time 2, \(\ldots, n\) at time \(n\) denoted by \((Ia)_\angl{n}\) is given by \[(Ia)^{i}_\angl{n} = \frac{\ddot{a}^{i}_{\actuarialangle{n}} - nv^n}{i}.\]

Notes
An increasing annuity but with payments in advance is given by \[(I\ddot{a})^{i}_\angl{n} = \frac{\ddot{a}^{i}_{\actuarialangle{n}} - nv^n}{d}.\]
The formulas for the accumulated values are \[(Is)^{i}_\angl{n} = \frac{\ddot{s}^{i}_{\actuarialangle{n}} - n}{i} \quad\text{(in arrears)}\] \[(I\ddot{s})^{i}_\angl{n} = \frac{\ddot{s}^{i}_{\actuarialangle{n}} - n}{d} \quad\text{(in advance)}\]
1.5.5 Compound increasing annuities
The following example considers the value of compound increasing annuities where the payments increase by a constant factor each time.
Example 1.35 Assume that the effective rate of interest is 6% p.a. Calculate the present value as at 1 January 2010 of an annuity payable annually in arrears for 8 years. The first payment is ฿10 and subsequent payments increase by 2% per annum compound.
Solution:

At 1/1/2010, the present value of the payment is given by \[\begin{aligned} PV &= 10 \cdot \frac{1}{1.06} + 10 \cdot \frac{1.02}{(1.06)^2} + \cdots + 10 \cdot \frac{(1.02)^7}{(1.06)^8} \\ &= \frac{10}{1.02} \left( \frac{1.02}{1.06} + \left( \frac{1.02}{1.06} \right)^2 + \cdots + \left( \frac{1.02}{1.06} \right)^8 \right)\end{aligned}\] The above equation can be arranged so that the annuity formula can be applied. We can define \(j\) such that \(1 + j = 1.06/1.02\), and hence, \[\begin{aligned} PV &= \frac{10}{1.02} \left( \frac{1}{1 + j} + \left( \frac{1}{1+j} \right)^2 + \cdots + \left( \frac{1}{1+j} \right)^8 \right) \\ &= \frac{10}{1.02} a_\angl{8} \quad \text{ at } j\% \\ &= \frac{10}{1.02} \left( \frac{1 - \left(\frac{1.02}{1.06}\right)^8 }{\left( \frac{1.06}{1.02} - 1 \right)} \right) \\ &= 66.2216\end{aligned}\]
1.5.6 Annuities payable more than once per time unit
Consider the value of an annuity payable in arrears \(m\) times per time unit at an effective rate of interest \(i\) per time unit. The annuity is still payable for \(n\) time units and a total amount of 1 unit per time unit. The present and accumulated values of the corresponding annuity are denoted by \(a^{(m)i}_\angl{n}\) and \(s^{(m)i}_\angl{n}\), respectively.
To calculate either the present or accumulation value of this annuity, we can simply apply the first principles by using the effective rate of interest per \(1/m\) time unit. In particular, we have \[a^{(m)i}_\angl{n} = \frac{1}{m} a^j_\angl{n\cdot m},\] and \[s^{(m)i}_\angl{n} = \frac{1}{m} s^j_\angl{n\cdot m},\] where \(j\) is the effective rate per \(1/m\) time unit.
Example 1.36 Calculate the accumulation at 1 January 2020 of an annuity of ฿100 per month, payable in arrears from 1 January 2010 at an effective rate of interest of 4% p.a.
Solution: The annual payment is 1200 and the effective rate per month equivalent to 4% p.a. is \(j = (1.04)^{1/12} - 1 = 0.003274\) per month. Hence, \[1200 s^{(12)4\%}_\angl{10} = 100 s^j_\angl{12\cdot 10} = 14669.59.\]
1.6 Nominal Rates of Interest
Nominal interest rates are the interest rates before taking inflation into account. They may also refer to the advertised (in bank accounts) or stated rates of interest on a loan, without regard to fees or compound interest. Throughout this section, the time unit used is assumed to be one year.
Effective rate of interest is the interest \(i\) paid at the end of the year on an amount ฿1 at the start of the year.
Nominal interest rate payable \(p\) times per period, denoted by \(i^{(p)}\) is an effective rate of interest of \(i^{(p)}/p\) applied for each \(p\)th of a period. The interest is paid more frequently than once per measurement period.
The nominal rate of interest payable \(p\) times per period is also known as the rate of interest convertible \(p\)thly or compounded \(p\)thly.
Example 1.37 A nominal rate of interest of \(i^{(4)} = 10\%\) p.a. convertible quarterly means an interest rate of 10/4 = 2.5% per quarter effective. Calculate the accumulated value in 1 year of a payment of ฿100 at the given nominal rate.
Solution: When working with the nominal interest rate, the nominal interest rate is often converted to an effective interest rate. In this example, the nominal interest rate \(i^{(4)} = 10\%\) is equivalent to an effective interest rate of \(2.5\%\) per quarter. The accumulated value in 1 year is \(100 (1 + 2.5\%)^4 = 110.3813\). After compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 10.3813 (or 10.3813%. p.a. effective)
Nominal is used where interest is paid more frequently than once per unit year.
Example 1.38 At a rate of 12% p.a. effective, draw a timeline to show cashflows if ฿100 is invested at the start of the year.
Solution: The accumulated value of ฿100 at the end of the year is \(100 (1 + 12\%) = 112\).
Example 1.39 At a rate of 12% p.a. compounding quarterly, draw a time line to show cashflows if ฿100 is invested at the start of the year.
Solution: The nominal interest rate \(i^{(4)} = 12\%\) is equivalent to an effective interest rate of \(3\%\) per quarter. The accumulated value in 1 year is \(100 (1 + 3\%)^4 = 112.55\). After compound interest is taken into account, the interest income of an investor at the quarterly convertible nominal interest rate of 10% p.a. is 12.55 (or 12.55%. p.a. effective)
\(i^{(p)}\) is an effective rate of interest of \(i^{(p)}/p\) applied for each \(p\)th of a period. The interest is paid more \(p\) times per measurement period (i.e. per year). The value at time can be regarded as the annuity having cashflow of \(i^{(p)}/p\) per each period as shown in the figure below. Therefore, the accumulated value in 1 year can also be calculated as \(100( 1 + 0.03 s_{\angl{4}}^{3\%})\).
Note In practice, it is easier to work with the effective rate of interest which is defined in a suitable time unit.
The following formula can be used to convert between the effective rate \(i\) p.a. and the nominal rate \(i^{(m)}\) p.a.: \[( 1 + i) = \left( 1 + \frac{i^{(m)}}{m}\right)^m.\]
- Example 1.40
Express a nominal annual interest rate of 9% convertible half-yearly as a monthly effective interest.
Express a two-monthly effective interest of 3% as a nominal annual interest rate convertible two-monthly.
Solution:
The effective rate \(i\)% p.a. is \[i = ( 1 + \frac{0.09}{2})^2 - 1.\] Hence the monthly effective rate is \(j = (1 + i)^{1/12} - 1 = ( 1 + \frac{0.09}{2})^{2/12} - 1 = 0.007363\).
A nominal annual interest rate convertible two-monthly is \(6 \cdot 3\% = 18\%\).
Example 1.41 Express each of the following effective rates per annum as a nominal rate, and vice versa.
| Effective Rate | Nominal Rate |
|---|---|
| \(i\) = 0.04 | \(i^{(4)} = 0.039412\) |
| \(i\) = 0.10 | \(i^{(12)} = 0.095690\) |
| \(i\) = 0.06152 | \(i^{(2)} = 0.06\) |
| \(i\) = 0.126825 | \(i^{(12)} = 0.12\) |
1.6.1 Nominal Rates of Discount
The effective rate of discount per annum is \(d = 1 -v\). It is the amount of interest payable at the start of the time unit which is equivalent to \(i\) payable at the end of the time unit.
The nominal rate of discount payable \(p\) times per period \(d^{(m)}\) (or convertible \(p\)thly or compounded \(p\)thly is interest of \(d^{(m)}/m\) paid at the start of each \(1/m\) of a year.
The relationship between the effective discount rate \(d\) p.a. and the nominal rate of discount payable \(m\) times a year is \[1 - d = \left(1 - \frac{d^{(m)}}{m}\right)^m.\]
- Example 1.42
Express a nominal annual discount rate of 6% convertible half-yearly as an annual effective discount.
Express an effective discount of 10% per half year as a nominal annual discount rate convertible quarterly.
Solution:
The annual effective discount \(d\) is \[d = 1- \left(1 - \frac{d^{(m)}}{m}\right)^m = 1- \left(1 - \frac{6\%}{2}\right)^2 = 0.0591 = 5.91\% \text{ per annum}.\]
We know that the discount factor \(v\) and the rate of discount \(d\) satisfy the following equation. \[v = 1- d.\] Hence the discount factor over half-year is \(1 - 0.1 = 0.9\). The discount factor \(v\) for one year (or 2 half-year) is \[(1-0.1)^2 = 0.9^2 = 0.81.\] It follows that the discount rate per annum is \(d = 1- 0.81 = 0.19\), and the nominal annual discount rate convertible quarterly \(d^{(4)}\) is given by \[\begin{aligned} d^{(m)} &= m \cdot \left( 1- (1 - d)^{1/m} \right) \\ d^{(4)} &= 4 \cdot \left( 1- (1 - 0.19)^{1/4} \right) = 0.205267. \end{aligned}\]
1.7 Principle of Equivalence, Yields and Equation of Value
The principle of equivalence is used to compare two different cashflows whether one is worth more than the other.
Consider two sequences of cashflows
\(C_1, C_2, \ldots\) with payments at times \(t_1, t_2, \ldots\) and
\(D_1, D_2, \ldots\) with payments at times \(s_1, s_2, \ldots\).
Assume that the interest rates are given and apply to both of them. The two sequences of cashflows are said to be equivalent (or equal in value) if their values at any time \(t\) are the same, i.e. there exists \(t \in \mathbb{R}\) such that \[PV^C(t) = PV^D(t).\]
Notes
If two sequences of cashflows have the same value at time \(s\), then they have the same value at any time \(t\) since
for \(t \le s\),
\(\text{(Value at time t)} = \text{(Value at time s)} \times V(t,s),\)
for \(t \ge s\)
\(\text{(Value at time t)} = \text{(Value at time s)} \times A(s,t).\)
The two sequences of cashflows are indifferent if their present values are the same.
The principle of equivalent can be applied for pricing a financial security, for example, a price \(P\) which will be paid by the investor in return for a series of future cashflows.
Example 1.43 Calculate the maximum price an investor wish to pay in return for an investment that will pay ฿500 at the end of each of the next 15 months given that the interest rate is 0.2% per month.
The present value of these payments of 500 at the end of the next 15 months is \[PV(0) = 500 a^{0.002}_{\angl{15}} = 500 \cdot \left( \frac{1 - (1.002)^{-15}}{0.002} \right) = 7381.35.\] Therefore, the investor would be willing to pay a maximum of 7381.35.
Example 1.44 Determine whether the following series of cashflows are equivalent given that an interest rate is 6% per annum effective.
One single payment of amount 6,691.127888 at year 5.
a level annuity of 300 payable yearly in arrears for the next 5 years plus a lump sum of 5,000.
a level annuity of 1,186.982002 payable yearly in arrears for the next 5 years.
Solution:
The present value is \(6,691.127888 \times (1.06)^{-5} = 5000\).
The present value is \[300 a^{0.06}_{\angl{5}} + 5000 \times (1.06)^{-5} = 5000.\]
The present value is \[1186.982002 a^{0.06}_{\angl{5}} = 5000.\]
Therefore, the three series of cashflows are indifferent.
1.7.1 Equation of value and yields
Consider a transaction from an investment that offers
to pay an investor of amounts (i.e. money received) \(B_1, B_2, \ldots, B_n\) at time \(t_1, t_2, \ldots ,t_n\)
in return for outlays (i.e. money paid out) of amounts \(A_1, A_2, \ldots, A_n\) at these times, respectively.
Only one of \(A_i\) and \(B_i\) will be non-zero in general.
An equation of value equates the present value of money received to the present value of money paid out, which can be written as \[\sum_{i=1}^n A_i v^i = \sum_{i=1}^n B_i v^i.\] The equation of value can also be written in terms of the net cashflow at time \(t_i\), i.e. \(C_t = B_t - A_t\), \[PV_i(0) = \sum_{i=1}^n C_i v^i =0.\]
Equations of value are used throughout actuarial work. Some examples are as follows:
The fair price to pay for an investment such as a fixed interest security or an equity (ie, \(PV\) outgo) equals the present value of the proceeds from the investment, discounted at the rate of interest required by the investor.
The premium for an insurance policy is calculated by equating the present value of the expected amounts received in premiums to the present value of the expected benefits and other outgo.
We shall be concerned mainly with the question:
At what rate of interest does the series of amounts paid out have the same value as the series of amounts received? The corresponding rate of interest is called the yield of the cashflows (or internal rate of return, money-weighted rate of return).
Notes
Equations of values may have no roots, a unique root or multiple roots.
In most practice situations, there is a unique positive real root.
Example 1.45 An investor pays ฿1,000 in order to receive ฿600 back in 2 years and ฿800 back in 4 years. Calculate the annual effective rate of interest earned on this investment (or the yield on the investment).
Solution: The yield of the investment \(i\%\) satisfies the equation of value \[PV_i(0) = -1000 + 600(1+i)^{-2} + 800(1+i)^{-4} = 0.\] To solve the equation for \(i\), we define \(z = (1+i)^{-2}\), resulting in \[8z^2 + 6z - 10 = 0.\] Therefore \(z = 0.804248\) and \(i = 0.115078.\)
Example 1.46 An investor pays ฿1,000 in order to receive ฿300 back at the end of the first 2 years and ฿400 back at the end of the third, forth and fifth year. Calculate the annual effective rate of interest earned on this investment (or the yield on the investment).
Solution: The yield of the investment \(i\%\) p.a. satisfies the equation of value \[PV_i(0) = -1000 + \frac{300}{(1+i)} + \frac{300}{(1+i)^{2}} + \frac{400}{(1+i)^{3}} + \frac{400}{(1+i)^{4}} + \frac{400}{(1+i)^{5}}.\] In our next section, we will learn how to approximate the yield of the above equation.
1.7.2 The method to estimate the yield
By using linear interpolation, the yield can be estimated as follows. Let \(P_1\) and \(P_2\) be the present values calculated at interest rates \(i_1\) and \(i_2\), respectively. Then the interest rate corresponding to a present value of \(P\) can be approximated by \[i \approx i_1 + (i_2 - i_1) \frac{P - P_1}{P_2 - P_1}.\] In order to apply this method to calculate the yield \(i\), we simply set \(P = 0\), and hence \[i \approx i_1 + (i_2 - i_1) \frac{ - P_1}{P_2 - P_1}.\]
From the figure above, the yield \(i\) can be approximated by \(i^*\), which is the \(x\)-intercept of the straight line joining the points \((i_1,P_1)\) and \((i_2,P_2)\). From \[\frac{i^* -i_1}{i_2 - i_1} = \frac{P_{i^*} - P_1}{P_2 - P_1},\] we have \(P_{i^*} = 0\) and \[i \approx i^* = i_1 + (i_2 - i_1) \frac{ - P_1}{P_2 - P_1}.\] Note that one can get a good approximation by taking values that are either side of the true value and about 1% apart.
Example 1.47 Approximate the yield of the transaction in Example 1.46.
Solution: Here, When \(i_1 = 0.21\), \(P_1 = PV_{0.21}(0) = 19.448\) and when \(i_1 = 0.22\), \(P_2 = PV_{0.22}(0) = -3.698.\) The yield is approximately equal to \[\begin{aligned} i &\approx 0.21 - (0.22 - 0.21) \left( \frac{19.448}{-3.698 - 19.448} \right) \\ &= 0.218402 \text{ p.a. effective.}\end{aligned}\]
1.8 Loan schedules
In this section, we describe how a loan may be repaid. A schedule of repayment together with the interest and capital components of an annuity payment will be discussed.
Suppose that a lender lends an individual of amount \(L\) for \(n\) years with an effective rate of interest \(i\) per annum. We say that the term of the loan is \(n\) years with the loan amount of \(L\). How could we repay the loan?
Repay as late as possible:
After \(n\) year, the borrower repays the entire loan and all interest that accrued over the period. The total amount to be repaid is equal to
Repay interest only during the term and repay the capital at the end of the term:
These types of loan where the borrower is a government or a company are bonds or fixed interest securities.
Repay loan by regular instalments of interest and capital throughout term of loan:
Each repayment must pay first for interest due and the remainder is used to repay some of the capital outstanding.
Example 1.48 You borrow ฿5,000 for a term of 3 years at a fixed interest rate of 10% pa. The loan is to be repaid by 3 level annual repayments of ฿2,010.57 at the end of each year. Calculate the interest content, capital content from each repayment and capital outstanding after such repayment.
Note The loan payments can be expressed in the form of a Loan Schedule as follows:
| Time | Repayment | Intest content | Capital content | Capital outstanding |
|---|---|---|---|---|
| 0 | 5000 | |||
| 1 | 2010.57 | 500 | 1510.57 | 3489.43 |
| 2 | 2010.57 | 348,943 | 1661.627 | 1827.80 |
| 3 | 2010.57 | 182.780 | 1827.79 | 0.01 |
1.8.1 The loan schedule
A more general form of loan payments can be expressed as follows: Let
\(L_t\) be the amount of the loan outstanding at time \(t\).
\(X_t\) be the instalment at time \(t\) (all instalments may not be the same amount).
\(i\) be the effective rate of interest per time unit charged on the loan.
ime Rep ayment Int est content Ca pital content Capital outstanding 0 \(L_0\) 1 $ X_1$ \(iL_0\) $ (X_1 - iL_0)$ \(L_1 = L_0 - (X_1 - iL_0)\) 2 $ X_2$ \(iL_1\) $ (X_2 - iL_1)$ \(L_2 = L_1 - (X_2 - iL_1)\) \(\vdots\) t $ X_t$ $ iL_{t-1}$ $(X t - iL{t-1})$ $L_ t = L_{t-1} - (X_t - iL_{t-1})$ \(\vdots\) n$ $ X_n$ $ iL_{n-1}$ $(X n - iL{n-1})$ 0
Note The capital outstanding after the \(k\)th payment is \(X a_{\angl{n-k}}\), which is the present value of future repayments. This holds even when the repayments and interest rates are not constant.
Example 1.49 A loan of ฿20,000 is repayable by equal monthly payments for 4 years, with interest rate payable at 10% pa effective.
Calculate the amount of each monthly payment.
Calculate the interest and capital contents of the 25th repayment.
Solution:
The loan is repaid by level instalments of amount \(X\) payable monthly. Working in months, we define \(j\%\) per month effective equivalent to 10% pa effective. We have \[j = (1.1)^{(1/12)} - 1 = 0.007974.\] The loan equation followed the equation of value is given by \[PV_j(0) = 20000 - X a^j_{\angl{48}} = 0\] Solving for \(X\) gives \(X =503.12\).
The capital outstanding after 24th repayment = \(L_{24} = X a^j_{\angl{24}} = 10950.23.\) Hence, the interest content of the 25th repayment = \(j \cdot L_{24} =87.32.\) The capital content of the 25th repayment = \(X =503.12 - 87.32 = 415.8.\)
1.8.2 Changing the term of a loan
The term of the loan can be changed in the following circumstances:
extend or shorten the term,
miss a number of payments,
repay part of the loan early.
The repayment amount will then need to be calculated according to the condition(s) as given in the change.
Example 1.50 A person takes out a loan of ฿100,000 to be repaid by level monthly instalments in arrears over 7 years where the bank charges an effective annual rate of interest of 6%
Calculate the monthly repayment Solution: Working in months, we define \(j\%\) per month effective equivalent to 6% pa effective. \[j = (1.06)^{(1/12)} - 1 = 0.007974.\] The loan equation followed the equation of value is given by \[PV_j(0) = 100000 - X a^j_{\angl{84}} = 0\] Solving for \(X\) gives \(X =1453.25\).
Calculate the new repayment amount if the the term of loan can be extended by 1 year, immediately after the 60th repayment has been made. Solution: The capital outstanding after 60th repayment = \(L_{60} = X a^j_{\angl{24}} = 32842.48.\) Now the remaining term becomes 3 years (or 36 months). The new repayment amount \(X'\) satisfies \[PV_j(0) = 32842.48 - X' a^j_{\angl{36}} = 0.\] Solving for \(X'\) gives \(X' = 996.77\).
Instead of extending the term, the person had requested to miss the 61st and 62nd repayments. Calculate the remaining installments. Solution: After missing the 61st and 62nd repayments, the capital outstanding at time 62 = \(L_{60}\cdot (1+j)^2 = 32842.48 (1.004868)^2 = 33162.99.\) Hence, the remaining number of payments is 22.
Calculate the new repayment amount if the person repaid ฿10,000 at the time he made the 60th repayment together with the 60th repayment. Solution: The revised capital outstanding after repayment of 10000 (the 60th repayment) is \(32842.48 - 10000 = 22842.48.\) The new repayment amount \(X''\) satisfies \[PV_j(0) = 22842.48 - X'' a^j_{\angl{24}} = 0.\] Solving for \(X''\) gives \(X'' = 1010.76\).
1.8.3 Changing the interest rate
The interest rates for a loan can vary during the term of the loan. The reasons for varying rates of interest could be the following:
interest rates have been planned to changed during the term, for example the borrower would repay less during the beginning of the loan, or
the lender changes the rates of interest to reflect the market conditions.
Example 1.51 You borrow ฿20,000 for a term of 20 years to be repaid by level annual instalments. The rate of interest will be 7% pa effective for the first 10 years and 8% pa effective thereafter. Calculate the annual repayment.
Solution: Let \(X\) be the annual repayment. Using an equation of value, we have \[20000 = X a^{7\%}_{\angl{10}} + (1.07)^{-10} X a^{8\%}_{\angl{10}}.\] Then solving for \(X\) gives \(X = 1916.69\).
Example 1.52 You borrow ฿20,000 for a term of 15 years to be repaid by level annual instalments where the bank charges an effective annual rate of interest of 6%. After the 10th repayment has been made, the bank raises the interest rate to 6.5% pa effective. Calculate the new repayment amount.
Solution: The annual repayment \(X\) for a term of 15 years before the adjustment of interest rate. \[X = \frac{20000}{a^{6\%}_{\angl{15}}} = 2059.26.\] However, after the 10th repayment has been made, the bank raises the interest rate to 6.5% pa effective. Therefore, the capital outstanding after the 10th repayment = \(L_{10} = X a^{6\%}_{\angl{5}} = 8674.332.\) After the adjustment of the interest rate, the new repayment amount \(X'\) satisfies satisfies \[PV_{6.5\%}(0) = 8674.332 - X' a^{6.5\%}_{\angl{5}} = 0.\] Solving for \(X'\) gives \(X' = 2087.34\).