Chapter 2 Bonds and Inflation
2.1 Bonds
A government or corporation can raise money in the capital markets by issuing fixed interest securities (FIS), also called bonds. Bonds are a form of medium and long-term securities.
This means that investors will lend money to the issuer (for e.g. the government or coporation) and in return will receive fixed interest payments known as coupons at fixed dates plus repayment of the loan at the end of the term.
Note The loan is usually split into smaller units that can be traded on a stock exchange. For example, a company raises ฿1,000,000,000 by issuing 10,000,000 bonds, each one a loan of face value ฿100. These can be bought and sold on a stock exchange.
2.1.1 Characteristics of Bonds
The nominal amount or face value of a bond is the amount of the loan it represents. The nominal amount is usually ฿1,000 (without further specific, we will set the nominal amount to be ฿100.)
The interest payments are called coupons, usually expressed as a percentage per year of the nominal amount. The rate of interest denoted by \(D\) is also known as coupon rate. They are always in arrears.
Coupons are usually expressed as the amount of interest payable in a year, but are paid half-yearly (twice per year) or quarterly (4 times per year)
Coupon dates are the dates on which the bond issuer will make interest payments.
Bonds have maturity dates at which point the principal amount must be paid back in full.
The loan is repaid or redeemed at the end of the term. The redemption amount per 100 nominal is the redemption rate, often expressed as a percentage.
A loan is redeemed
at a premium if redemption rate > 100%
at par if redemption rate = 100%
at a discount if redemption rate < 100%
Many corporate and government bonds are publicly traded; others are traded only over-the-counter (OTC) or privately between the borrower and lender.
Example 2.1 Each bond of ฿100 nominal value carries coupons of 6% pa payable half-yearly.
Solution: The coupon rate of 6% pa payable half-yearly means that bondholders will receive \[ \frac{6\%}{2} \times 100 = ฿ 3 \text{ every half-year}.\]
Example 2.2 An investor purchases ฿95 for a 5-year fixed interest bond with face value (or nominal amount of) ฿100. The bond pays coupon of 6% pa half-yearly in arrear and the lump sum equal to the nominal amount in 5 years’ time. The cashflows related to the payments of the bond can be shown as follows:
Solution: Cashflows are given in the following table.
| Time (year) | 0 | 0.5 | 1 | 1.5 | \(\ldots\) | 5 |
|---|---|---|---|---|---|---|
| Cashflow | -95 | 3 | 3 | 3 | \(\ldots\) | \(3 + 100\) |
Examples of bonds include
domestic bonds issued in the domestic currency such as gilts issued by UK government and treasury bonds issued by US government.
Eurobonds where an issuer sells the bond outside the domestic country.
debenture bonds issued by corporations.
Example 2.3 A company issues a 10-year bond, to be redeemed at 102%, with coupon of 6% pa payable half-yearly in arrears. The nominal amount of each bond is ฿100. What repayments are made?
Solution: Cashflows are given in the following table.
| Time (year) | 0 | 0.5 | 1 | 1.5 | \(\ldots\) | 9.5 | 10 |
|---|---|---|---|---|---|---|---|
| Cashflow | \(P\) | 3 | 3 | 3 | \(\ldots\) | \(3\) | \(3 + 102\) |
Here the bond price in the table above is denoted by \(P\).
The following questions may be asked:
At what price should be paid by an investor to obtain a net yield of \(i\) per annum?
Given the price of the fixed interest bond, what is the net yield per annum will be obtained?
2.1.2 Bond prices
Given a yield \(i\%\), the price of a bond can be computed by discounting all the future payments received net of any tax.
Example 2.4 A tax-exempt investor buy the bond in Example 2.3 on its issue date. Calculate the price the investor should pay to obtain a yield of 9%.
Solution: Appplying the Principle of Equivalence: by equate the present value of the future incomes at 9% with the unknown price \(P\).
\[P = \frac{6}{2} a^j_{\angl{20}} + 102 (\frac{1}{1.09})^{20},\] where \(j = (1.09)^{(1/2)} - 1 = 0.044031.\) This gives \(P = 82.44\). It should be emphasised that the price in this example differs from the nominal amount of 100.
Example 2.5 Refer to Examples 2.3 and 2.4. After the 10th coupon has been paid, the investor sells the bond. At that time the market yield on comparable 5-year bonds is 7% pa effective.
Calculate the price that he will obtain.
Calculate the yield that the first investor obtains if he paid ฿82.44 and received 10 coupon payments of ฿3 each and sold the bond after 5 years at the price of ฿97.75.
Solution:
- The remaining payments are shown in the table below.
| Time (half-year) | 10 | 11 | 12 | 13 | \(\ldots\) | 19 | 20 |
|---|---|---|---|---|---|---|---|
| Cashflow | \(-\) | 3 | 3 | 3 | \(\ldots\) | \(3\) | \(3 + 102\) |
Working in unit of half-year, we first calculate the effective rate per half-year, denoted by \(k\), that is equivalent to \(i = 7\%\).
\[ k = (1.07)^{(1/2)} - 1 = 0.034408. \]
The price \(P'\) that he will obtain follows from the following equation. \[P' = 3 a^k_{\angl{10}} + 102 (\frac{1}{1.07})^{5} = 97.75.\]
- The payments of the investor are shown in the table below.
| Time (half-year) | 0 | 1 | 2 | 3 | \(\ldots\) | 9 | 10 |
|---|---|---|---|---|---|---|---|
| Cashflow | -82.44 | 3 | 3 | 3 | \(\ldots\) | \(3\) | \(3 + 97.75\) |
Let \(i\) denote the yield (per half-year) that the first investor obtains. Working at time 10, the equation of value of the cashflows is \[ f(i) = 82.44 (1+i)^{10} - 3 s^i_{\angl{10}} - 97.75 = 0.\] By linear interpolation, we have \[ f(0.05) = -1.1976, \quad f(0.06) = 10.3451, \] and hence, the approximate of \(i\) is \(i^* \approx 0.051038\). The annual yield is then approximately equal to \((1 + 0.051038)^2 - 1 = 10.468\%\)
Notes
If the investor is not subject to taxation, the yield is called the gross yield.
The yield obtained by holding the bond until redemption is called redemption yield. This is quoted in financial newspapers.
If a bond is sold before redemption, the yield that the investor obtains is called realised yield. This yield depends on both the buying and selling prices.
Notes
There is an inverse relationship between the bond prices and yields.
The nominal amount of the loan is just a theoretical figure on which the coupon and redemption rates are based.
The amount of capital the borrower can actually raise on the issue date is the price that investors are willing to pay for the future income stream and also set by supply and demand.
The investors also consider the credit risk of the borrower. It is the risk that they might default on interest and capital payments.
The greater the credit risk, the higher the yield they will require.
The bonds can be traded on an exchange at any time until it is redeemed. The prices will depend on the remaining term to redemption and market conditions such as the yields obtainable on other investments.
2.1.3 No tax
A tax-exempt investor receives the full amount of the coupon and redemption payments. The price of an \(n\) year fixed interest bond which pays coupons of \(D\) per annum payable \(p\) thly in arrear and has redemption amount \(R\) is \[P = D a_{\angln}^{(p)} + R v^n\] at rate \(i\) per annum.
In practice, we can calculate by using a suitable time period, for example a period of half a year as shown in the previous examples. Then the formula can be written as \[P = \frac{D}{2} a_{\angl{2n}} + R v^{2n}\]
2.1.4 Income tax
Suppose an investor is subject to income tax at rate \(t_1\) on the coupons, which is due at the time that the coupons are paid. Tax will affect both yields and bond prices. In general, the price of this bond, an \(n\) year fixed interest bond which pays coupons of \(D\) per annum payable \(p\) thly in arrear and has redemption amount \(R\) is \[P = (1 - t_1) D a_{\angln}^{(p)} + R v^n\] at rate \(i\) per annum. Here the rate is called the net yield.
Example 2.6 An investor liable to income tax at 30% buys a 15-year fixed interest bond which is redeemable at par and pays coupons of 8% pa half-yearly in arrear. Calculate the price the investor should pay to obtain a net yield of 9% pa.
Solution: Coupon payments after tax are \[ (1 - t_1) D = (1 - 0.3) \frac{8\%}{2} \times 100 = 2.8.\]
The payments of the investor are shown in the table below.
| Time (half-year) | 0 | 1 | 2 | 3 | \(\ldots\) | 29 | 30 |
|---|---|---|---|---|---|---|---|
| Cashflow | \(P\) | 2.8 | 2.8 | 2.8 | \(\ldots\) | 2.8 | \(2.8 + 100\) |
The price the investor should pay to obtain a net yield of 9% pa can be calculated from \[P = 2.8 a^j_{\angl{30}} + 100 (\frac{1}{1+j})^{30} = 73.59,\] where where \(j = (1.09)^{(1/2)} - 1 = 0.044031\) per half-year effective.
2.1.5 Capital gains tax (CGT)
Capital gains tax is a tax levied on the capital gain made on the redemption of a bond (or the sale of the bond if sold earlier). The capital gain is simply the difference between
Note that capital gain refers to an increase in a capital asset’s value and is considered to be realized when the asset is sold. A capital loss is incurred when there is a decrease in the capital asset value compared to an asset’s purchase price.
Example 2.7 An investor liable to the capital gains tax at 20% purchases two bonds
Bond A for the price of ฿102 and
Bond B for the price of ฿98.
Calculate the capital gains tax on each bond if the investor sells them both one year later for ฿100 each.
Solution:
Bond A: Tax payment is \(0.2 \times \max\{100 - 102,0 \} = 0\) (i.e. capital loss)
Bond B: Tax payment is \(0.2 \times \max\{100 - 98,0 \} = 0.4\) (i.e. capital gain)
Here we assume that no ‘relief’, i.e. we cannot add the two bonds together and say we bought the two bonds for ฿200 and sold the bonds for ฿200.
Notes
Similar to income tax, the price of the bond is then calculated on the net redemption received after tax has been deducted.
When the purchase and sale (or redemption) prices are known, it it easy to calculate the yield.
In contrast, as the price depends on whether there is a capital gain and the capital gain depends on the price, it is not easy to calculate the price for a given redemption yield. There is a test to determine whether CGT is payable.
Example 2.8 An investor liable to the capital gains tax at 20% purchases a 10-year bond with an annual coupon of 8% pa payable yearly in arrear, to be redeemed at par.
Calculate the redemption yield the investor obtain if the price is ฿96 per ฿100 nominal.
What price should the investor pay to obtain a yield of 7% pa effective? (see note below)
What price should the investor pay to obtain a yield of 9% pa effective?
Solution:
- The bond is redeemed at par. Therefore, the redemption amount is 100 THB which is greater than the bond price, and the capital gain tax is payable.
The payments of the investor are shown in the table below.
| Time (year) | 0 | 1 | 2 | 3 | \(\ldots\) | 9 | 10 |
|---|---|---|---|---|---|---|---|
| Cashflow | -96 | 8 | 8 | 8 | \(\ldots\) | 8 | 8 + 100 - 0.2(100 - 96) |
Let \(i\) denote the yield per year that the first investor obtains. Working at time 10, the equation of value of the cashflows is \[ f(i) = -96 (1+i)^{10} + 8 s^i_{\angl{10}} + 99.2 = 0.\] By linear interpolation, we have \[ f(0.08) = 7.836, \quad f(0.09) = -6.523, \] and hence, the approximate of \(i\) is \(i^* \approx 0.08546 = 8.546\%\).
- We know that \(P = 96\) is equivalent to yield approximately equal to \(8.546\%\).
To obtain a yield of \(7\%\), this should imply that \(P > 96\). If \(P \ge R = 100\), no CGT is payable. This would change the equation we need to calculate the bond price. Two cases to be considered are
CGT is payable: The equation of value is \[ P = 8 a^i_{\angl{10}} + 99.2\cdot (1+i)^{-10}, \quad i = 7\%\]
CGT is not payable: The equation of value is \[ P = 8 a^i_{\angl{10}} + 100\cdot (1+i)^{-10}, \quad i = 7\%\]
Note In this example, we can guess whether CGT is payable because we have calculated the price to yield 8.546% from the above question. Then we can use the appropriate equation to calculate the bond price and check whether or not our initial guess was correct.
According to the note, let us guess that \(P > 100\), i.e. CGT is not payable.
\[ P = 8 a^i_{\angl{10}} + 100\cdot (1+i)^{-10}, \quad i = 7\%,\] which implies that \(P = 107.02 > 100\). So our initial guess was correct and CGT is not payable.
- Here \(9\% > 8.546\%\). Let us guess that \(P < 100\), i.e. CGT is payable. \[ P = 8 a^i_{\angl{10}} + 99.2\cdot (1+i)^{-10}, \quad i = 7\%,\] which implies that \(P = 92.99 < 100\). So our initial guess was correct and CGT is payable.
Note The algorithm to test whether CGT will be payable will be discussed elsewhere in the course “Theory of Interest”.
2.2 Inflation
Inflation is a measure of the rate of change in the price of consumer goods and services, such as food and beverages, transportation and housing.
In Thailand or US, it is measured with reference to a consumer price index (or CPI). In UK, it is measured in terms of retail price index (RPI).
Bureau of Trade and Economic Indices reports the CPI on a monthly basis.
High inflation means that prices increase quickly and hence the purchasing power significantly decreases.
Let \(Q(t)\) be the CPI at time \(t\). Then the rate of inflation per year denoted by \(q(t)\) is \[q(t) = \frac{Q(t)}{Q(t-1)} - 1.\] The average inflation rate per year between time \(s\) and \(t\), denoted by \(\bar{q}\), satisfies \[(1 + \bar{q})^{t-s} = \frac{Q(t)}{Q(s)},\] and hence \[\bar{q} = \left( \frac{Q(t)}{Q(s)} \right)^{1/(t-s)} - 1.\]
Example 2.9 A set of goods costs ฿98.25 in January 2013 and ฿101.44 in January 2018. Calculate the average inflation rate \(\bar{q}\) over this period.
Solution: The increase from Jan 2013 to Jan 2018 (5 years) is \[\frac{101.44}{98.25} - 1 = 0.032.\] The average of inflation rate \(\bar{q}\) is given by \[(1 + \bar{q})^5 = 1.032.\] Therefore \(\bar{q} = 0.64\%\).
Therefore, ฿1 in January 2013 buys as much as ฿1.032 in January 2018.
The following table shows the monthly consumer price indices from January 2011 to December 2019. Source: http://www.price.moc.go.th/
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 91.93 | 92.3 | 92.75 | 94.03 | 94.35 | 94.47 | 94.64 | 95.05 | 94.73 | 94.91 | 95.12 | 94.66 |
| 2012 | 95.03 | 95.38 | 95.95 | 96.35 | 96.73 | 96.89 | 97.22 | 97.61 | 97.93 | 98.06 | 97.71 | 98.09 |
| 2013 | 98.25 | 98.46 | 98.52 | 98.68 | 98.92 | 99.07 | 99.17 | 99.16 | 99.32 | 99.49 | 99.59 | 99.73 |
| 2014 | 100.15 | 100.39 | 100.6 | 101.1 | 101.51 | 101.4 | 101.32 | 101.23 | 101.06 | 100.96 | 100.84 | 100.33 |
| 2015 | 99.74 | 99.86 | 100.03 | 100.05 | 100.22 | 100.32 | 100.25 | 100.03 | 99.98 | 100.18 | 99.86 | 99.47 |
| 2016 | 99.21 | 99.36 | 99.57 | 100.11 | 100.68 | 100.71 | 100.36 | 100.32 | 100.36 | 100.52 | 100.46 | 100.59 |
| 2017 | 100.75 | 100.79 | 100.33 | 100.49 | 100.64 | 100.66 | 100.53 | 100.64 | 101.22 | 101.38 | 101.45 | 101.37 |
| 2018 | 101.44 | 101.21 | 101.12 | 101.57 | 102.14 | 102.05 | 102.00 | 102.27 | 102.57 | 102.63 | 102.40 | 101.73 |
| 2019 | 101.71 | 101.95 | 102.37 | 102.82 | 103.31 | 102.94 | 103.00 | 102.80 | 102.90 | 102.74 | 102.61 | 102.62 |
Figure 2.1 shows the monthly consumer price indices from January 2011 to December 2019.
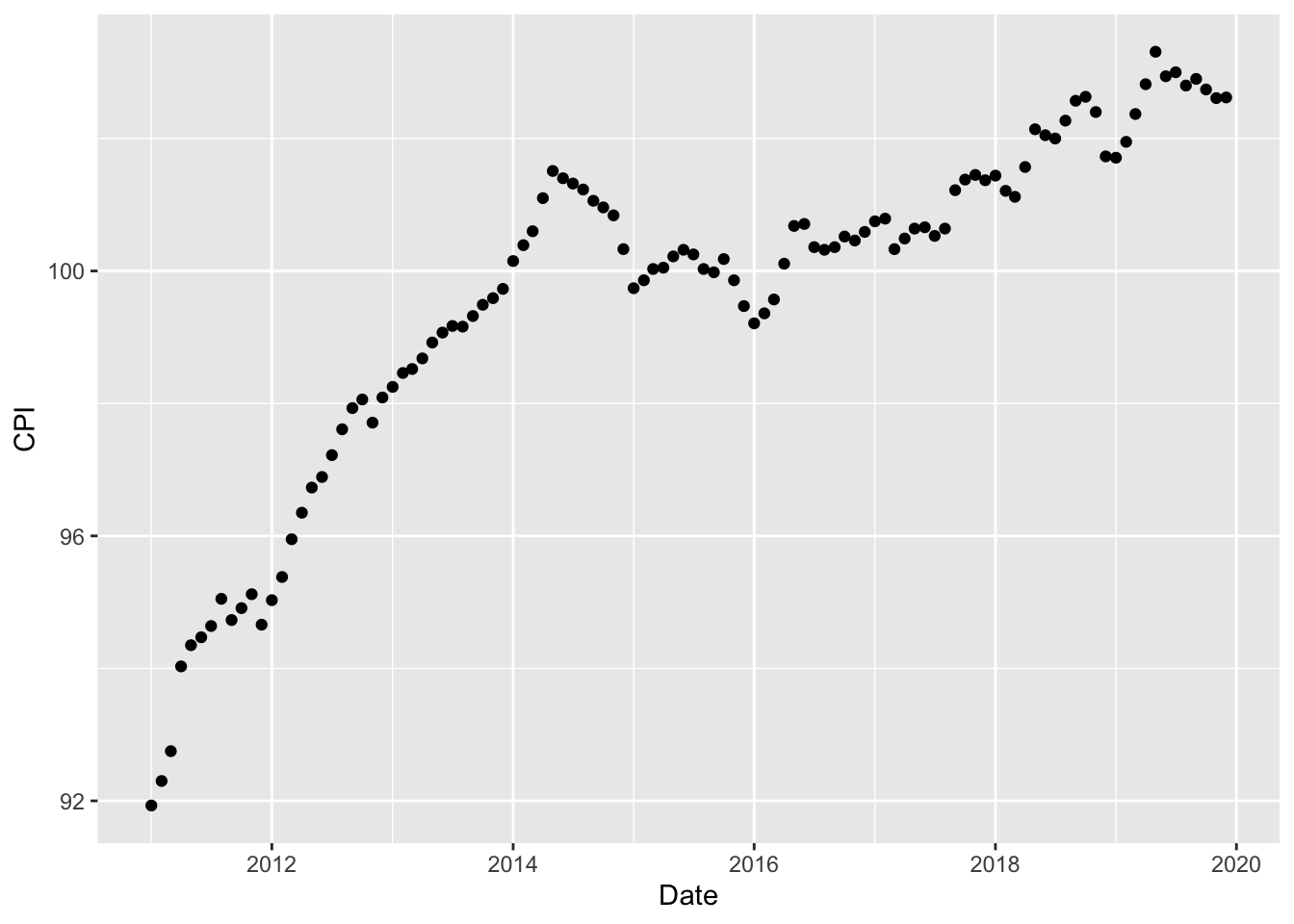
Figure 2.1: The monthly consumer price indices from January 2011 to December 2019
Example 2.10 An investment contract made on January 2018 promises to pay an investor of ฿10,000 in 5 years’ time. Assume the average inflation rate at \(\bar{q} = 0.64\%\) for the next 5 years.
If a bowl of noodles costs ฿100 in 2018, then ฿10,000 could buy 100 bowls. How many bowls of noodles would the payment of ฿10,000 buy in the next 5 years?
Solution: In Jan 2018, ฿100 buys as much as \(100 (1.0064)^5 =\) ฿103.2 in Jan 2023.
So ฿10000 in Jan 2023 could buy \[\frac{10000}{103.2} \approx 96 \text{ bowls}.\] Notice that we divide by \((1 + \bar{q})^5\) to calculate how much your money is worth at the end of the next five years.
The quantity of goods that can be bought with 10,000 in January 2023 reduces from 100 to 96 bowls.
The effect of inflation results in the reduction of the purchasing power of a unit of money in January 2023 compared to that in January 2018.
The amount of ฿10,000 is referred to as the monetary (or nominal) payment in 5 years. This is the amount of money that change hands.
The real payment of ฿10,000 (due at time 5 years) in time 0 unit is \[\begin{aligned} 10000 \frac{Q(0)}{Q(5)} &= 10000 \frac{1}{(1.0064)^5} \\ &= 9686.05.\end{aligned}\] Here we have less purchasing power with your money at the end of the five years than you had at the start of the year.
The real payment (in time 0) is the purchase power of 10,000 paid in 5 years relative to today. It is the amount of cash in hand at the end of the period reduced for the effects of inflation.
In general, ฿X at time \(t\) has the purchasing power relative to time \(s\) of \[X \cdot \frac{Q(s)}{Q(t)}.\]
2.2.1 Real rates of interest
The rate of interest which is calculated using monetary payments is called a money (or monetary or nominal) rate of interest.
The real rate of interest is calculated using real payments.
Example 2.11 An investor deposits 100 at time 0 and receives 120 after one year.
The monetary rate of interest effective is \[\frac{120}{100} - 1 = 20\%.\]
Suppose that the inflation rate over this one year period is 4%. Calculate the real payment of 120 at time 1 and the real rate of interest. After adjusting for the inflation rate, the real rate of interest can be calculated by first expressing both payments in units of the same purchasing power.
In term of time 0 money unit, the transaction is represented by
Here, the real payment of 120 due in 1 year in terms of time 0 unit is \(\displaystyle{120 \cdot \frac{1}{1.04} = 115.38}\). Hence the real rate of interest is 15.38%.
In term of time 1 money unit, the transaction is represented by
Similarly, we instead calculate the real payment of 100 relative to time 1, which gives \(100 \cdot 1.04 = 104\). The real rate of interest is \[\frac{120}{104} - 1 = 15.38\%,\] which is the same as the previous case.
2.2.2 Real yields
It is often useful to look at the rate of return earned on an investment after taking into account of inflation. As analogous to the real rate of interest, a real yield is calculated using real payments, which can be obtained by expressing payments in units of the same purchasing power at some specific date.
Example 2.12 A 5-year bond with nominal value of ฿100 was issued in January 2013. The coupon rate was 8% p.a. payable yearly in arrears. Redemption was at par after 5 years. The bond was issued at 100%. Calculate the yield to a non-tax paying investor
in monetary terms Solution:
The transaction together with the inflation indices \(Q(t)\) at time \(t\) is shown as follows:
Clearly, the monetary rate of return on this transaction is 8%. This is because the investor receives the interest payment of ฿8 at the end of each year plus the initial capital of ฿100 at the end of five years.
Alternatively, one can solve for the monetary rate of return from the following equation of value \[f(i) = -100 + 8 a^i_{\actuarialangle{5}} + 100\frac{1}{(1+i)^5} = 0.\]
in real terms with reference to the CPI.
Taking into account of the inflation rates, we calculate the real payment in term of time 0 unit by dividing the monetary amounts by the proportional increase in the inflation index from 0 to \(t\).
| Time | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| Cashflow | -100 | 8 | 8 | 8 | 8 | 8 + 100 |
| CPI | 98.25 | 100.15 | 99.74 | 99.21 | 100.75 | 101.44 |
| Real value of cashflow at \(t = 0\) | -100 | \(8 \cdot \frac{98.25}{100.15}\) = 7.85 | \(8 \cdot \frac{98.25}{99.74}\) = 7.88 | \(8 \cdot \frac{98.25}{99.21}\) = 7.91 | \(8 \cdot \frac{98.25}{100.75}\) = 7.80 | \(8 \cdot \frac{98.25}{101.44}\) | = 104.60 |
The real yield \(i'\) p.a. effective solve the equation of value as follows: \[f(i') = -100 + 7.85 v + 7.88v^2 + 7.91v^3 + 7.80v^6 + 104.6v^5 = 0,\] which gives \(i' \approx 7.30\%\) by the linear interpolation.
In general, the real yield \(i'\) for a series of cashflows \(C(t_1), C(t_2), \ldots, C(t_n)\), given associated inflation index \(Q(t_k)\) for \(k = 1, \ldots, n\), can be obtained in terms of time 0 money units as \[\sum_{k=1}^n C(t_k) \frac{Q(0)}{Q(t_k)} \frac{1}{(1 + i')^{t_k}} = 0.\] This is equivalent to \[\sum_{k=1}^n C(t_k) \frac{1}{Q(t_k)} \frac{1}{(1 + i')^{t_k}} = 0.\] Therefore, the real yield is independent of the date the payment units are adjusted to.
2.2.3 Calculating real yields given constant inflation assumptions
For future cashflows, the inflation index will not be known. Suppose we assume a constant rate of inflation \(q\) p.a. The cashflows \(C(t_k)\) at time \(t_k\) have the purchasing power at time 0 (or real payments relative to time 0) \[\begin{aligned} C(t_k) \cdot \frac{Q(0)}{Q(t_k)} &= C(t_k) \cdot \frac{Q(0)}{Q(0)(1+q)^{t_k}} = C(t_k) \cdot \frac{1}{(1+q)^{t_k}} , \quad k = 1, \ldots, n.\end{aligned}\] The relation between the real yield \(i'\), the constant rate of inflation \(q\) and the monetary yield \(i\) can be obtained as follows: From the equation of value, \[\begin{aligned} 0 &= \sum_{k=1}^n C(t_k) \frac{Q(0)}{Q(t_k)} \frac{1}{(1 + i')^{t_k}} \\ &= \sum_{k=1}^n C(t_k) \cdot \frac{1}{(1+q)^{t_k}}\cdot \frac{1}{(1 + i')^{t_k}}\end{aligned}\] With no inflation adjustment, the monetary rate of return \(i\) satisfies \[0 = \sum_{k=1}^n C(t_k) \cdot \frac{1}{(1+i)^{t_k}}.\] Therefore, if we assume a constant rate of inflation \(q\) p.a., then the following relation holds: \[(1 +i) = ( 1 + q)(1+i').\] This provides the relationship between the real yield \(i'\), the monetary yield \(i\) and the inflation rate \(q\).
2.2.4 Index-linked securities
An index-linked security is an investment security in which interest payments and the redemption are adjusted in line with inflation index values by linking the payments to the Consumer Price Index (CPI). The reasons for these types of security are
to protect investors against inflation risk, and
to help pension funds to provide index-link benefits so that the index-link liability can be matched with the index-link asset.
Example 2.13 Consider an index-link bond of a nominal of ฿100 issued at time \(t_0\), bearing an annual coupon of \(C\%\) payable \(m\) times a year and a redemption is at \(R\%\). Then per ฿100 nominal, the monetary amount (actual cashflow) of an interest payment \(D(t_k)\) at time \(t_k\) is
The monetary amount of the redemption amount at time \(t_n\) is
Example 2.14 An investor purchased a 3-year index-linked bond in January 2015. The investor received payments at the end of each year plus a final redemption amount, all of which were adjusted in line with the CPI values reported in Table 2.1. Calculate the actual payments received by the investor.
Note In practice, due to delays in calculating the index, the payments (or cashflows) will be adjusted based on the inflation index value from an earlier period.
Let \(s\) denote the indexation time lag. The payments are adjusted with reference to inflation index value at time \(s\) (months) before the payment is made. Then the monetary amount of an interest payment \(D(t_k)\) per ฿100 nominal at time \(t_k\) is \[\displaystyle D(t_k) = 100 \frac{C}{m} \cdot \frac{Q(t_k - \frac{s}{12})}{Q(t_0 - \frac{s}{12})}\] and the monetary amount of redemption at time \(t_n\) is \[D(t_n) = 100 R \cdot \frac{Q(t_n - \frac{s}{12})}{Q(t_0 - \frac{s}{12})}.\] The term \(Q(t_0 - \frac{s}{12})\) is called the base inflation figure (the base CPI figure).
Example 2.15 Repeat Example2.14 for a 3-year index linked bond. The indexation adjustments are made according to the CPI three months before each payment, i.e. \(s = 3\) months.
Example 2.16 In January 2015, the government issued an index-linked bond of term 10 years. Coupons are payable half-yearly in arrears, and the annual nominal coupon rate is 4%. The coupons and redemption amount are adjusted with reference to the inflation index value 3 months before the payment is made.
Assume the constant inflation rate from February 2018 is 2% p.a.
Find the base CPI figure (i.e. it is the October 2014 CPI which is 3 months before the issue date).
Calculate the actual payments received by the investor.
Assume that the price of ฿100 nominal of this index-linked bond in January 2018 (after the January 2018 coupon payment) is ฿ . Calculate the monetary yield that an investor who purchased the bond in January 2018 (after the January 2018 coupon payment) will obtained.
Calculate the real yield for this investor under the above assumptions.