บทที่ 4 การประยุกต์ของอนุพันธ์ (Applications of Differentiation)

4.1 Applications of derivatives related to students discipline

จากบทเรียนก่อนหน้านี้ เราทราบว่าถ้าตัวแปร \(y\) สามารถเขียนอธิบายได้ด้วยฟังก์ชันๆ หนึ่ง ที่ขึ้นกับตัวแปร \(x\) นั่นคือ \(f(x)\) เราจะสามารถวาดกราฟของ \(y\) หรือฟังก์ชัน \(f(x)\) ได้ และถ้าเราทราบว่า จุด \(P(x_0,y_0)\) และจุด \(Q(x_1,y_1)\) ต่างอยู่บนกราฟของ \(y\) แสดงว่า \(y_0=f(x_0)\) และ \(y_1=f(x_1)\) นั่นเอง ความชันของเส้นตรงที่ลากผ่านจุด \(P\) และจุด \(Q\) มักใช้ \(m\) เป็นสัญลักษณ์ มีสูตรการหาดังนี้ \[m=\frac{\triangle y}{\triangle x}=\frac{y_1-y_0}{ x_1-x_0}=\frac{f(x_1)-f(x_0)}{ x_1-x_0}=\frac{y_0-y_1}{ x_0-x_1}\] ความชันของเส้นตรงที่กล่าวมาแล้วนี้ มีชื่อเรียกอีกชื่อหนึ่งว่า อัตราการเปลี่ยนแปลงเฉลี่ยของ \(f(x)\) ตั้งแต่ \(x=x_0\) จนถึง \(x=x_1\) และ \[\lim_{x_1 \rightarrow x_0} \frac{f(x_1)-f(x_0)}{ x_1-x_0} =f'(x_0)\] คืออัตราการเปลี่ยนแปลงของ \(f(x)\) ณ \(x=x_0\) หรือการหาอนุพันธ์ของฟังก์ชัน \(f(x)\) เทียบกับตัวแปร \(x\) เมื่อ \(x\) มีค่าเท่ากับ \(x_0\) นั่นเอง

หลักการหาอนุพันธ์สามารถนำไปประยุกต์ใช้ได้ในหลากหลายสาขาวิชาชีพ ไม่ว่าจะเป็นธุรกิจ เศรษฐศาสตร์ วิศวกรรมศาสตร์ ฟิสิกส์ เคมี หรือแม้กระทั่งชีววิทยา สำหรับบทนี้ ผู้เขียนจะขอกล่าวถึง การนำแนวคิดทางคณิตศาสตร์นี้ไปประยุกต์ใช้กับปัญหาทางวิทยาศาสตร์ชีวภาพ เพื่อให้สอดคล้องกับความสนใจของผู้เรียน

ตัวอย่าง 4.1 AIDS ย่อมาจาก acquired immunodeficiency syndrome เป็นโรคติดต่อทางเพศสัมพันธ์และการให้เลือด ซึ่งพบการแพร่ระบาดมาตั้งแต่ปี พ.ศ. 2523 โดยผู้ป่วยที่เป็นโรค AIDS จะพบเชื้อไวรัส HIV ใน antibodies ซึ่งไวรัส HIV นี้มีระยะฟักตัวตั้งแต่ไม่กี่เดือน จนกระทั่งนานนับปี นักวิจัยคนหนึ่งนำเชื้อไวรัส HIV มาเพาะเลี้ยงในจานเพาะเชื้อ พบว่า ขนาดของประชากรไวรัส ณ เวลา \(t\) , \(N(t)\) สอดคล้องกับสมการ \(N(t)=1000+20t+t^2\) อยากทราบว่าไวรัสชุดนี้มีอัตราการเปลี่ยนแปลง ณ \(t\) ใดๆ เป็นอย่างไร

กำหนดให้ \(t\) แทน เวลา \(N(t)\) แทน ขนาดของประชากรไวรัส ณ เวลา \(t\) จากการทดลองพบว่า ขนาดของประชากรไวรัส ณ เวลา \(t\) ใดๆ สอดคล้องกับสมการ \[N(t)=1000+20t+t^2\] ดังนั้น อัตราการเปลี่ยนแปลงของขนาดของประชากรไวรัส ณ เวลา \(t\) ใดๆ คือ \[\frac{dN}{dt}=20+2t\]

ตัวอย่าง 4.2 จากการสำรวจพบว่า จำนวนผู้ป่วยด้วยโรค AIDS, \(P(t)\) มีความสัมพันธ์กับสมการ \[P(t)=100t^2-2t^3\] เมื่อ \(t\) เป็นเวลาที่ผ่านไปนับจากวันนี้ มีหน่วยเป็นวัน อยากทราบว่าเมื่อ 20 วันผ่านไป จะมีผู้ป่วยด้วยโรคนี้กี่คน และมีอัตราการเพิ่มจำนวนผู้ป่วยเป็นเท่าไหร่

กำหนดให้ \(t\) แทน เวลา มีหน่วยเป็นวัน \(P(t)\) แทน จำนวนผู้ป่วยด้วยโรค AIDS มีหน่วยเป็นคน จากการสำรวจพบว่า \[P(t)=100t^2-2t^3\] เมื่อ 20 วันผ่านไป แสดงว่า \(t=20\) จะได้ว่า \(P(20)=100(20)^2-2(20)^3=24,000\) ดังนั้น เมื่อ 20 วันผ่านไป จะมีผู้ป่วยโรค AIDS 24,000 คน อัตราการเพิ่มจำนวนผู้ป่วยโรค AIDS ณ เวลา \(t\) ใดๆ หาได้ดังนี้ \[\frac{dP}{dt}=200t-6t^2\] ดังนั้น เมื่อ 20 วันผ่านไป อัตราการเพิ่มจำนวนผู้ป่วยจะมีค่าเท่ากับ \(200(20)-6(20)^2\) หรือ \(1,600\) คนต่อวัน

ตัวอย่าง 4.3 จากการศึกษาทางสิ่งแวดล้อมระบุว่า \(Q(t)\) ระดับ carbon monoxide (CO) เฉลี่ยในอากาศ (หน่วยเป็น ppm) จะมีค่าเป็นเท่าไร \[Q(t)=0.05t^2+0.1t+3.4\] เมื่อ \(t\) เป็นเวลาที่นับจากนี้เป็นต้นไป มีหน่วยเป็นปี อยากทราบว่า ระดับ CO เฉลี่ยในอากาศจะเปลี่ยนแปลงไปอย่างไร ในอีก 2 ปี ข้างหน้า

กำหนดให้ \(t\) เป็นเวลาที่นับจากวันนี้ มีหน่วยเป็นปี \(Q(t)\) เป็นระดับ CO เฉลี่ยในอากาศมีหน่วยเป็น ppm จากการศึกษาทางสิ่งแวดล้อมระบุว่า \[Q(t)=0.05t^2+0.1t+3.4\] อัตราการเปลี่ยนแปลงระดับ CO เฉลี่ยในอากาศ ณ \(t\) ใดๆ คือ \[\frac{dQ}{dt}=0.1t+0.1\] ในอีก 2 ปีข้างหน้า \(t=2\) \[\frac{dQ}{dt}=0.1(2)+0.1=0.3>0\] ระดับ CO เฉลี่ยในอากาศจะเพิ่มขึ้น (เพราะ \(\displaystyle\frac{dQ}{dt}>0\)) ด้วยอัตราเร็ว 0.3 ppm ต่อปี

ตัวอย่าง 4.4 Poiseuille’s law กล่าวว่า ความเร็วของเลือด (หน่วย คือ เซนติเมตรต่อวินาที) ที่อยู่ห่างจากจุดกึ่งกลางของหลอดเลือด \(r\) เซนติเมตร มีสูตรดังนี้ \(S(r)=C(R^2-r^2)\) เมื่อ \(C\) เป็นค่าบวกใดๆ และ \(R\) เป็นรัศมีของหลอดเลือด อยากทราบว่า ความเร็วของเลือดจะเปลี่ยนแปลงเป็นอย่างไร เมื่อเลือดอยู่บริเวณกึ่งกลางระหว่างจุดกึ่งกลางและผนังของหลอดเลือด

กำหนดให้ \(r\) เป็นระยะห่างจากจุดกึ่งกลางของหลอดเลือด (หน่วยเป็นเซนติเมตร) \(S(r)\) เป็นความเร็วของเลือด ณ \(r\) ใดๆ (หน่วยเป็นเซนติเมตรต่อวินาที) จาก Poiseuille’s law \[S(r)=C(R^2-r^2)\] อัตราการเปลี่ยนแปลงความเร็วของเลือด ณ \(r\) ใดๆ คือ \[\frac{dS}{dr}=-2Cr\] เลือดที่อยู่บริเวณกึ่งกลางระหว่างจุดกึ่งกลางและผนังของหลอดเลือดหมายถึง \(r=\frac{R}{2}\) ดังนั้น \[\frac{ds}{dr}\bigg{|}_{r=R/2} = - CR < 0 \text{ เพราะว่า } C>0, R>0\] แสดงว่าความเร็วของเลือดจะลดลง (เพราะ \(\displaystyle\frac{dS}{dr}<0\)) ด้วยอัตรา \(CR\) (cm/s)/cm

4.1.1 แบบฝึกหัด

1. ผลการทดลองแสดงให้เห็นว่า ความเข้มข้นของปริมาณ adrenaline ที่ฉีดเข้าไปในร่างกาย, \(x\), มีความสัมพันธ์กับการตอบสนองของกล้ามเนื้อ, \(y\), ด้วยสมการ \(y=\frac{x}{a+bx}\) เมื่อ \(a\) และ \(b\) เป็นค่าคงตัว จงหาอัตราการเปลี่ยนแปลงการตอบสนองของกล้ามเนื้อ เมื่อเทียบกับความเข้มข้นของปริมาณ adrenaline ที่ฉีดเข้าไปในร่างกาย

2. กำหนดให้ \(\displaystyle P(t)=\frac{1000t}{t+10}\) แสดงถึงขนาดของประชากรแบคทีเรีย เมื่อ \(t\) เป็นเวลา จงหาอัตราการเจริญเติบโตของประชากร

3. Schuty - Borisoff laws กล่าวถึง ปริมาณ substrate, \(y\), ที่ถูกเปลี่ยนรูปด้วยเอนไซม์ ในรูปของฟังก์ชันที่ขึ้นกับเวลา \(t\) ดังนี้ \[y=k\sqrt{cat}\] เมื่อ \(k\), \(a\), \(c\) เป็นค่าคงตัว จงหาอัตราการเปลี่ยนแปลงปริมาณ substrate ที่ถูกเปลี่ยนรูปด้วยเอนไซม์ ณ เวลา \(t\) ใดๆ

4.2 Sketching the graph of a function from the derivative

ในหัวข้อนี้เราใช้ประโยชน์จากเรื่อง derivative ในการวาดกราฟของฟังก์ชัน เมื่อนึกถึงกราฟของฟังก์ชัน เราสนใจลักษณะที่สำคัญ เช่นช่วงใดที่กราฟเพิ่ม ช่วงใดที่กราฟลด ค่าสูงสุดและค่าต่ำสุดของกราฟอยู่ที่ใด กราฟมีลักษณะคว่ำในช่วงใด หรือมีลักษณะหงายในช่วงใด เป็นต้น

แนวคิดแรกคือเรื่องของการเพิ่มและลดของฟังก์ชัน เรามารู้จักนิยามก่อน

นิยาม 4.1 ให้ \(f\) เป็นฟังก์ชันนิยามบนช่วง \(I\) ให้ \(x_1\) และ \(x_2\) เป็น สมาชิกในช่วง \(I\)

• \(f\) เป็นฟังก์ชันเพิ่มบนช่วง \(I\) ก็ต่อเมื่อ ถ้า \(x_1 < x_2\) แล้ว \(f(x_1) < f(x_2)\)

• \(f\) เป็นฟังก์ชันลดบนช่วง \(I\) ก็ต่อเมื่อ ถ้า \(x_1 < x_2\) แล้ว \(f(x_1) > f(x_2)\)

• \(f\) เป็นฟังก์ชันคงตัวบนช่วง \(I\) ก็ต่อเมื่อ สำหรับค่า \(x_1\) และ \(x_2\) ใด ๆ แล้ว \(f(x_1) = f(x_2)\)

ประโยชน์ของ derivative ที่ใช้ในการตรวจสอบการเพิ่มและลดของฟังก์ชัน มาจาก ทฤษฏีบท :

ทฤษฎี 4.1 ให้ \(f\) เป็นฟังก์ชันต่อเนื่องบนช่วงปิด \([a,b]\) และหา derivative ได้ บนช่วงเปิด \((a,b)\)

1. ถ้า \(f'(x) > 0\) สำหรับทุก ๆ \(x \in (a,b)\) แล้ว \(f\) เป็น ฟังก์ชันเพิ่มบนช่วง \([a,b]\)

2. ถ้า \(f'(x) < 0\) สำหรับทุก ๆ \(x \in (a,b)\) แล้ว \(f\) เป็น ฟังก์ชันลดบนช่วง \([a,b]\)

3. ถ้า \(f'(x) = 0\) สำหรับทุก ๆ \(x \in (a,b)\) แล้ว \(f\) เป็น ฟังก์ชันคงตัวบนช่วง \([a,b]\)

ทฤษฏีบทนี้สามารถขยายผลจากช่วง \([a,b]\) ไปได้ถึงช่วงในรูป \([a,\infty)\), \((-\infty,b]\) และ \((-\infty,\infty)\)

ตัวอย่าง 4.5 พิจารณาฟังก์ชัน \[f(x) = x^2-3x+2\] เราหา derivative ของฟังก์ชัน ได้ว่า \(f'(x) = 2x-3\) ซึ่งบอกเราว่า \[\begin{equation} \begin{aligned} f'(x) &< 0 \text{ สำหรับ $x < 3/2$} \\ f'(x) &> 0 \text{ สำหรับ $x > 3/2$} \end{aligned} \end{equation}\] เนื่องจาก \(f\) เป็นฟังก์ชันต่อเนื่องที่ \(x=3/2\) เราจึงบอกได้ว่า \[\begin{equation} \begin{aligned} \text{ $f$ เป็นฟังก์ชันลดบนช่วง $(-\infty,3/2]$} \\ \text{ $f$ เป็นฟังก์ชันเพิ่มบนช่วง $[3/2,\infty)$} \end{aligned} \end{equation}\]

แนวคิดต่อไป เป็นเรื่องของลักษณะหงายหรือคว่ำของกราฟของฟังก์ชัน ถ้ากราฟของฟังก์ชันมีลักษณะหงาย เราเรียกว่าฟังก์ชัน concave up ในขณะที่ถ้ากราฟของฟังก์ชันมีลักษณะคว่ำ เราเรียกว่า ฟังก์ชัน concave down นิยามที่ชัดเจนของ concavity ของฟังก์ชันเป็นดังนี้

นิยาม 4.2 ให้ \(f\) เป็นฟังก์ชันซึ่งหา derivative ได้บนช่วงเปิด \(I\)

• \(f\) concave up บนช่วง \(I\) ถ้า \(f'\) เป็นฟังก์ชันเพิ่มบนช่วง \(I\)

• \(f\) concave down บนช่วง \(I\) ถ้า \(f'\) เป็นฟังก์ชันลดบนช่วง \(I\)

ลักษณะ concavity ของฟังก์ชัน สามารถตรวจสอบโดยใช้ derivative ดังนี้

ทฤษฎี 4.2 ให้ \(f\) เป็นฟังก์ชันซึ่งหา derivative อันดับสองได้บนช่วง \(I\)

1. ถ้า \(f''(x) > 0\) บนช่วง \(I\) แล้ว \(f\) concave up บนช่วง \(I\)

2. ถ้า \(f''(x) < 0\) บนช่วง \(I\) แล้ว \(f\) concave down บนช่วง \(I\)

ตัวอย่าง 4.6 พิจารณาฟังก์ชัน \(f(x) = x^2-3x+2\) ถ้าเราคำนวณ derivative อับดับสอง \(f''(x) = 2\) ซึ่งจากทฤษฏีบท เราบอกได้ว่า \(f\) concave up บนช่วง \((-\infty,\infty)\)

การเปลี่ยนทิศทางของ concavity ของฟังก์ชัน ก็เป็นอีกที่หนึ่งของกราฟของ ฟังก์ชัน ซึ่งมีลักษณะเด่น ที่จุดนี้กราฟอาจมีการเปลี่ยนจากลักษณะหงาย เป็นคว่ำ หรือจากลักษณะคว่ำเป็นหงาย

นิยาม 4.3 ถ้า \(f\) เป็นฟังก์ชันต่อเนื่องบนช่วงเปิด \(I\) ซึ่งมี \(x_0\) เป็น สมาชิก และ \(f\) เปลี่ยนทิศทางของ concavity ที่จุดนี้ แล้วเรากล่าว ว่า \(f\) มี inflection point ที่ \(x_0\) และเราเรียก \((x_0,f(x_0))\) ว่า inflection point ของ \(f\)

ตัวอย่าง 4.7 ฟังก์ชัน \(f(x) = x^3\) มี \[f'(x) = 3x^2, \quad f''(x) = 6x\] สังเกตว่า

• เมื่อ \(x<0\), \(f''(x) < 0\)

• เมื่อ \(x>0\), \(f''(x) >0\)

ดังนั้น ที่จุด \(x=0\), \(f\) มีการเปลี่ยนทิศทางของ concavity จาก concave down เมื่อ \(x<0\) เป็น concave up เมื่อ \(x>0\) เพราะฉะนั้น inflection point จึงเป็น \((0,0)\) สังเกตอีก ว่า \(f\) เป็นฟังก์ชันเพิ่มตลอดช่วง \((-\infty,\infty)\)

ค่าสูงสุดและต่ำสุดในย่านหนึ่ง ๆ ของกราฟก็เป็นอีกลักษณะเด่น ที่เราสามารถ ตรวจสอบได้โดยใช้ derivative ของฟังก์ชัน

นิยาม 4.4

1. ฟังก์ชัน \(f\) มี relative maximum ที่ \(x_0\) ถ้ามีช่วงเปิดที่มี \(x_0\) เป็นสมาชิก และ \(f(x_0) \ge f(x)\) สำหรับทุก ๆ \(x\) ที่เป็น สมาชิกในช่วงเปิดดังกล่าว

2. ฟังก์ชัน \(f\) มี relative minimum ที่ \(x_0\) ถ้ามีช่วงเปิดที่มี \(x_0\) เป็นสมาชิก และ \(f(x_0) \le f(x)\) สำหรับทุก ๆ \(x\) ที่เป็น สมาชิกในช่วงเปิดดังกล่าว

3. ถ้า \(f\) มี relative maximum หรือ relative minimum ที่ \(x_0\) แล้ว เรากล่าวว่า \(f\) มี relative extremum ที่ \(x_0\)

ฟังก์ชันหนึ่ง ๆ อาจมี relative maximum, relative minimum หลายที่ อาจมีที่เดียว หรืออาจไม่มีเลยก็ได้ ดังตัวอย่างต่อไปนี้

ตัวอย่าง 4.8

1. ฟังก์ชัน \(f(x) = (x-1)^2\) มี relative minimum ที่ \(x=1\) แต่ไม่มี relative maximum

2. ฟังก์ชัน \(f(x) = x^3\) ไม่มี relative extremum

3. ฟังก์ชัน \(f(x) = \frac{1}{3}x^3 - \frac{1}{2}x^2\) มี relative maximum ที่ \(x=0\) และมี relative minimum ที่ \(x=1\)

4. ฟังก์ชัน \(f(x) = \sin x\) มี relative maxima ที่ \(\pi/2 + 2n\pi\) และมี relative minima ที่ \(3\pi/2 + 2n\pi\) สำหรับทุก ๆ จำนวนเต็ม \(n\) ใด ๆ

ทฤษฎี 4.3 ถ้า \(f\) มี relative extremum ที่จุด \(x_0\) แล้ว \(f'(x_0) = 0\) หรือ \(f\) หา derivative ไม่ได้ที่ \(x_0\)

นิยาม 4.5 เราเรียก \(x_0\) ว่า critical point ของฟังก์ชัน \(f\) ถ้า \(f'(x_0) = 0\) หรือ \(f\) หา derivative ไม่ได้ที่ \(x_0\)

ตัวอย่าง 4.9 ฟังก์ชัน \(f(x) = |x^2-x|\) มี critical point ที่จุด \(x=0,1\) และฟังก์ชัน \(g(x) = x^2-x\) ก็มี critical point ที่จุด \(x=0,1\) เช่นกัน สังเกตว่า ฟังก์ชัน \(f\) หา derivative ไม่ได้ที่จุด \(x=0,1\) ในขณะที่ฟังก์ชัน \(g\) หา derivative ได้ ที่จุดดังกล่าว

การตรวจสอบหา relative extremum โดยใช้ derivative เราใช้ทฤษฏีบทต่อไปนี้

ทฤษฎี 4.4 ให้ \(f\) เป็นฟังก์ชันต่อเนื่องที่ critical point \(x_0\) และถ้า ค่าของ \(f'\) เปลี่ยนเครื่องหมายที่ \(x_0\) แล้ว \(f\) มี relative minimum หรือ relative maximum ที่ \(x_0\)

1. ถ้า \(f'\) มีค่าเป็นลบสำหรับค่าทางซ้ายของ \(x_0\) และมีค่า เป็นบวกสำหรับค่าทางขวาของ \(x_0\) แล้ว \(f\) มี relative minimum ที่ \(x_0\)

2. ถ้า \(f'\) มีค่าเป็นบวกสำหรับค่าทางซ้ายของ \(x_0\) และมีค่า เป็นลบสำหรับค่าทางขวาของ \(x_0\) แล้ว \(f\) มี relative maximum ที่ \(x_0\)

ตัวอย่าง 4.10 พิจารณาฟังก์ชัน \(f(x) = |x^2-x|\) จงหาค่า \(x\) ที่ทำให้ \(f\) มี relative extrema

วิธีทำ เรารู้ว่า \(x=0,1\) เป็น critical point เขียนฟังก์ชัน \(f\) ใหม่ว่า \[f(x) = |x||x-1| = \begin{cases} x(x-1) & \text{ $x \le 0$} \\ -x(x-1) & \text{ $0< x \le 1$} \\ x(x-1) & \text{ $x > 1$} \end{cases}\] นั่นคือ \[f'(x) = \begin{cases} 2x-1 & \text{ $x < 0$} \\ -2x+1 & \text{ $0 < x < 1$} \\ 2x-1 & \text{ $x> 1$} \end{cases}\] ดังนั้นที่จุด \(x\) ใกล้ ๆ \(0\) และ \(x<0\) เราพบว่า \(f'(x) < 0\) ในขณะที่ที่จุด \(x\) ใกล้ ๆ \(0\) และ \(x>0\) เราพบว่า \(f'(x) > 0\) เราจึงสรูปว่า \(f\) มี relative minimum ที่ \(0\) ในทำนองเดียวกัน ที่จุด \(x\) ใกล้ ๆ \(1\) และ \(x<1\) เราพบว่า \(f'(x) < 0\) ในขณะที่ที่จุด \(x\) ใกล้ ๆ \(1\) และ \(x>1\) เราพบว่า \(f'(x) > 0\) เราจึงสรูปได้เช่นกันว่า \(f\) มี relative minimum ที่ \(1\)

เมื่อเราพิจารณาฟังก์ชัน แล้วต้องการวาดกราฟของฟังก์ชัน เราคงจำได้ว่า มีข้อมูล บางประการที่เราสามารถตรวจสอบได้ก่อน เช่น \(x\)-intercepts \(y\)-intercepts ลักษณะ ของกราฟเมื่อ \(x\) เข้าใกล้ค่าอนันต์ เป็นต้น ตัวอย่างต่อไปนี้ เราจะใช้ความรู้เหล่านี้ ประกอบกับเรื่องของ derivative ในการวาดกราฟของฟังก์ชัน

ตัวอย่าง 4.11 จงวาดกราฟของฟังก์ชัน \[y = f(x) = x^3-3x+2\]

วิธีทำ

• \(x\)-intercepts: ให้ \(y=0\) ได้ว่า \[\begin{equation} \begin{aligned} x^3-3x+2 &= 0 \\ (x+2)(x^2-2x+1) &= 0 \\ (x+2)(x-1)^2 &= 0 \end{aligned} \end{equation}\] ดังนั้น \(x=-2, 1\)

• \(y\)-intercepts: ให้ \(x=0\) ได้ว่า \(y=2\)

• ลักษณะกราฟเมื่อ \(x \to \infty\) และ \(x \to -\infty\): สังเกตว่า \[\begin{equation} \begin{aligned} \lim_{x\to \infty} (x^3-2x+2) = \infty \\ \lim_{x\to -\infty} (x^3-2x+2) = -\infty \end{aligned} \end{equation}\]

• ช่วงการเพิ่มและการลดของฟังก์ชัน เราหา derivative ของ \(f\) ได้ว่า \[\frac{dy}{dx} = 3x^2-3 = 3(x-1)(x+1)\] ดังนั้น \(f\) จึงเป็นฟังก์ชันเพิ่มเมื่อ \(x < -1\) เป็นฟังก์ชันลดเมื่อ \(-1 < x < 1\) และ เป็นฟังก์ชันเพิ่มอีกครั้งเมื่อ \(x>1\)

• ช่วงการ concave up และ concave down ของฟังก์ชัน \(f\) เราหา derivative อันดับ สองของฟังก์ชัน \(f\) ได้ว่า \[\frac{d^2y}{dx^2} = 6x\] ดังนั้น \(f\) จึง concave up เมื่อ \(x>0\) และ concave down เมื่อ \(x<0\) ฟังก์ชัน \(f\) มี inflection point ที่ \(0\)

จากข้อมูลทั้งหมด เราเขียนกราฟคร่าว ๆ ดังรูปที่ 4.1

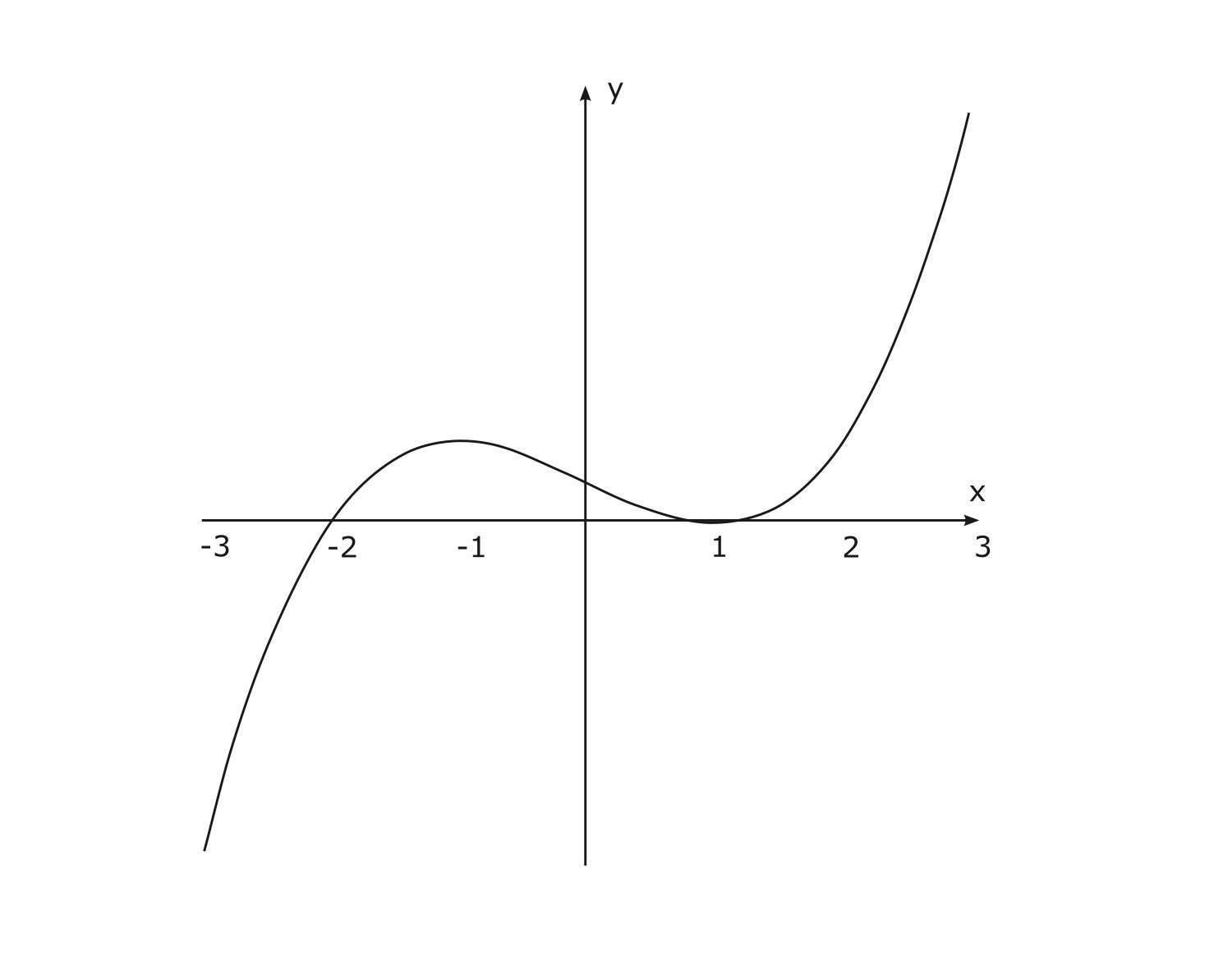
Figure 4.1: กราฟของฟังก์ชัน \(f(x) = x^3 - 3x + 2\)

ตัวอย่าง 4.12 ถ้า \(f\) เป็นฟังก์ชัน และเรามีข้อมูลที่เกี่ยวกับ \(f'\) ดังนี้

1. \(f'(x) > 0\) และ \(f'\) เป็นฟังก์ชันเพิ่มในช่วง \((-\infty, -1)\)

2. \(f'(x) > 0\) และ \(f'\) เป็นฟังก์ชันลดในช่วง \((-1,1)\)

3. \(f'(1) = 0\)

4. \(f'(x) < 0\) และ \(f'\) เป็นฟังก์ชันลดในช่วง \((1,\infty)\)

จงวาดกราฟที่เป็นไปได้ของฟังก์ชัน \(f\)

วิธีทำ จากข้อมูลที่ได้มา เราสรูปว่า

1. \(f\) เป็นฟังก์ชันเพิ่ม และ concave up ในช่วง \((-\infty,-1)\)

2. \(f\) เป็นฟังก์ชันเพิ่ม และ concave down ในช่วง \((-1,1)\)

3. \(f\) มี relative maximum ที่ \(x=1\)

4. \(f\) เป็นฟังก์ชันลด และ concave down ในช่วง \((1,\infty)\)

ตัวอย่างกราฟของฟังก์ชัน \(f\) เช่นรูป 4.2

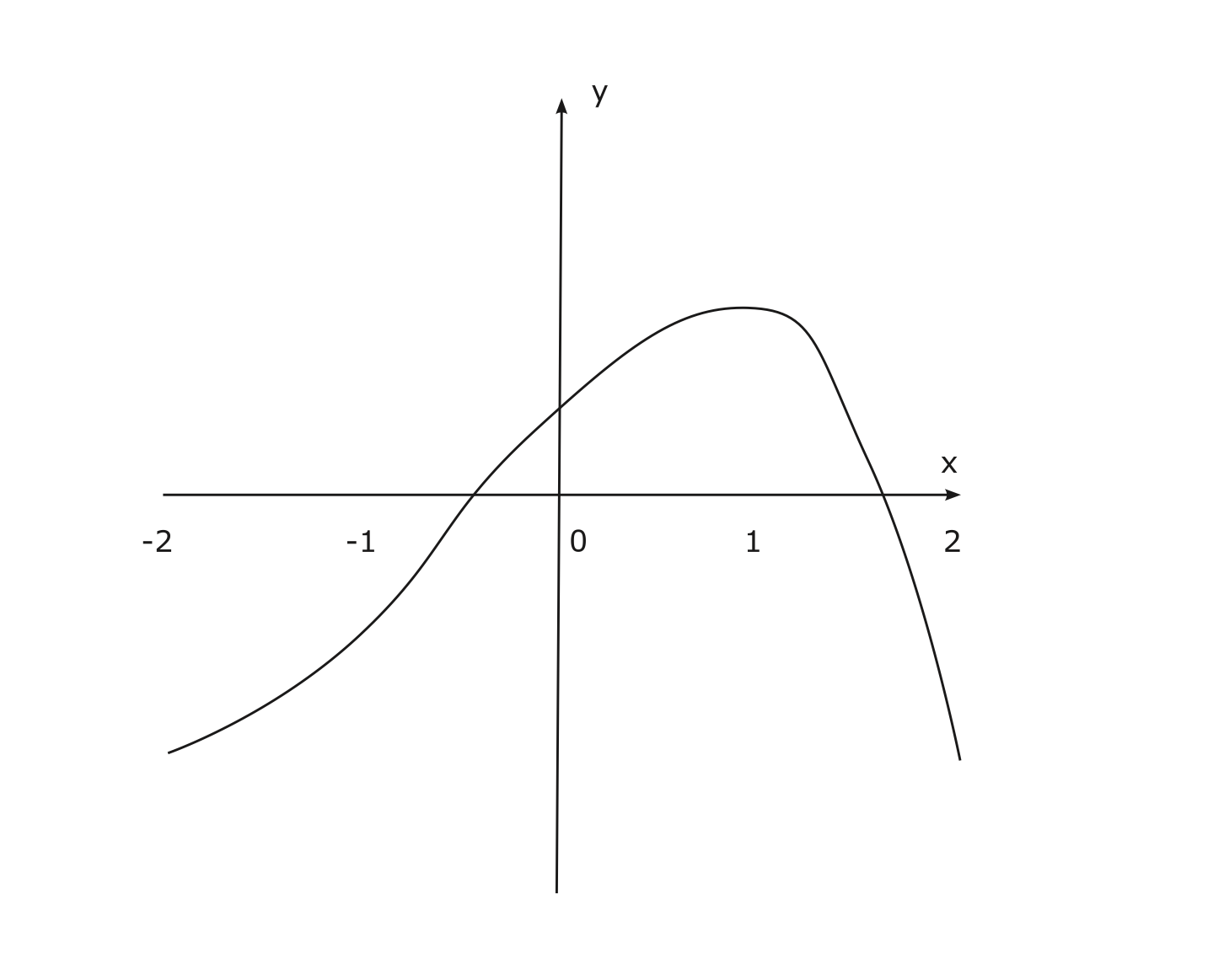
Figure 4.2: กราฟของฟังก์ชัน \(f\) จากข้อมูลที่กำหนด

ตัวอย่าง 4.13 พิจารณาฟังก์ชัน \[f(x) = \frac{x}{x^2+1}\]

วิธีทำ

• \(x\)-intercepts: ให้ \(y=0\) ได้ว่า \[\begin{equation} \begin{aligned} \frac{x}{x^2+1} &= 0 \\ x &= 0 \end{aligned} \end{equation}\]

• \(y\)-intercepts: ให้ \(x=0\) ได้ว่า \(y=0\)

• ลักษณะกราฟเมื่อ \(x \to \infty\) และ \(x \to -\infty\): สังเกตว่า \[\begin{equation} \begin{aligned} \lim_{x\to \infty} \frac{x}{x^2+1} = 0 \\ \lim_{x\to -\infty} \frac{x}{x^2+1} = 0 \end{aligned} \end{equation}\]

• ช่วงการเพิ่มและการลดของฟังก์ชัน เราหา derivative ของ \(f\) ได้ว่า \[\frac{dy}{dx} = \frac{1-x^2}{(x^2+1)^2} =\frac{(1-x)(1+x)}{(x^2+1)^2}\] ดังนั้น \(f\) จึงเป็นฟังก์ชันลดเมื่อ \(x < -1\) เป็นฟังก์ชันเพิ่มเมื่อ \(-1 < x < 1\) และ เป็นฟังก์ชันลดอีกครั้งเมื่อ \(x>1\)

• ช่วงการ concave up และ concave down ของฟังก์ชัน \(f\) เราหา derivative อันดับ สองของฟังก์ชัน \(f\) ได้ว่า \[\frac{d^2y}{dx^2} = \frac{2x^3-6x}{(x^2+1)^3} = \frac{2x(x-\sqrt{3})(x+\sqrt{3})}{(x^2+1)^3}\] ดังนั้น \(f\) จึง concave up เมื่อ \(x>\sqrt{3}\) หรือเมื่อ \(-\sqrt{3}<x<0\) ในขณะที่ \(f\) concave down เมื่อ \(x<-\sqrt{3}\) หรือเมื่อ \(0<x<\sqrt{3}\) ฟังก์ชัน \(f\) มี inflection point ที่ \(0,\pm\sqrt{3}\)

จากข้อมูลทั้งหมด เราเขียนกราฟคร่าว ๆ ดังรูป 4.3

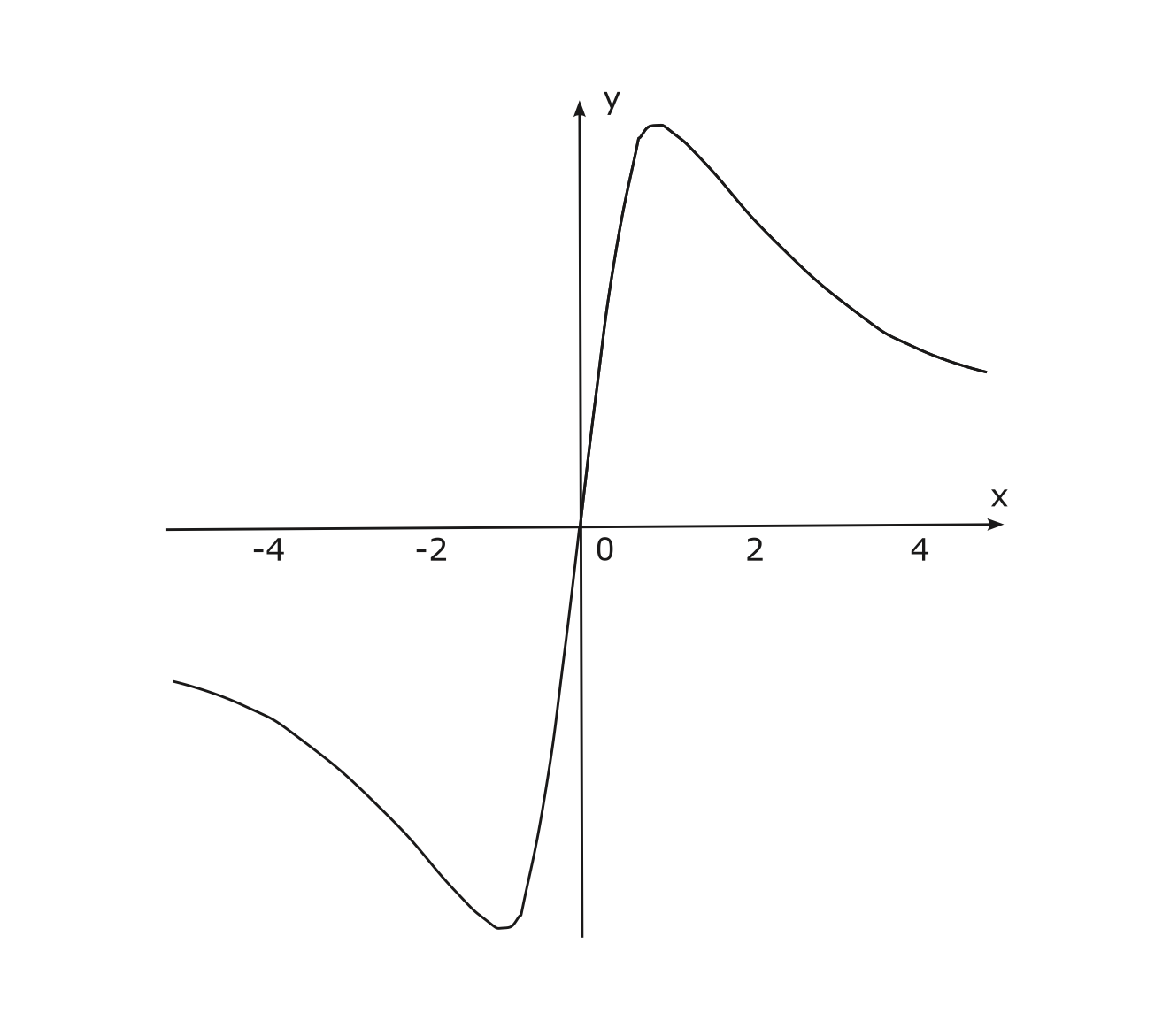
Figure 4.3: กราฟของฟังก์ชัน \(f(x) = \frac{x}{x^2+1}\)

ตัวอย่าง 4.14 พิจารณาฟังก์ชัน \[f(x) = \ln(x^3+1)\] นิยามบนช่วง \((-1,\infty)\) จงวาดกราฟของฟังก์ชันนี้

วิธีทำ

• \(x\)-intercepts: ให้ \(y=0\) พบว่า \(x=0\)

• \(y\)-intercepts: ให้ \(x=0\) พบว่า \(y=0\)

• ลักษณะกราฟเมื่อ \(x \to \infty\): \[\lim_{x\to\infty} \ln(x^3+1) = \infty\]

• ลักษณะกราฟเมื่อ \(x\to (-1)^+\): \[\lim_{x\to (-1)^+} \ln(x^3+1) = -\infty\]

• ช่วงการเพิ่มและการลดของฟังก์ชัน เราหา derivative ของ \(f\) ได้ว่า \[f'(x) = \frac{3x^2}{x^3+1} > 0\] สำหรับ \(x>-1\) ดังนั้น \(f\) เป็นฟังก์ชันเพิ่มตลอดโดเมน

• ช่วงการ concave up และ concave down ของฟังก์ชัน \(f\) เราหา derivative อันดับ สองของฟังก์ชัน \(f\) ได้ว่า \[f''(x) = \frac{-3x^4+6x}{(x^3+1)^2} = \frac{-3x(x-\sqrt[3]{2})(x^2+\sqrt[3]{2}x+\sqrt[3]{4})}{(x^3+1)^2}\] ดังนั้น \(f\) จึง concave up เมื่อ \(0<x<\sqrt[3]{2}\) และ \(f\) concave down เมื่อ \(x<0\) หรือเมื่อ \(x>\sqrt[3]{2}\) ฟังก์ชัน \(f\) มี inflection point ที่ \(0,\sqrt[3]{2}\) ค่าของ \(\sqrt[3]{2} \approx 1.26\)

จากข้อมูลทั้งหมด เราเขียนกราฟคร่าว ๆ ดังรูป 4.4

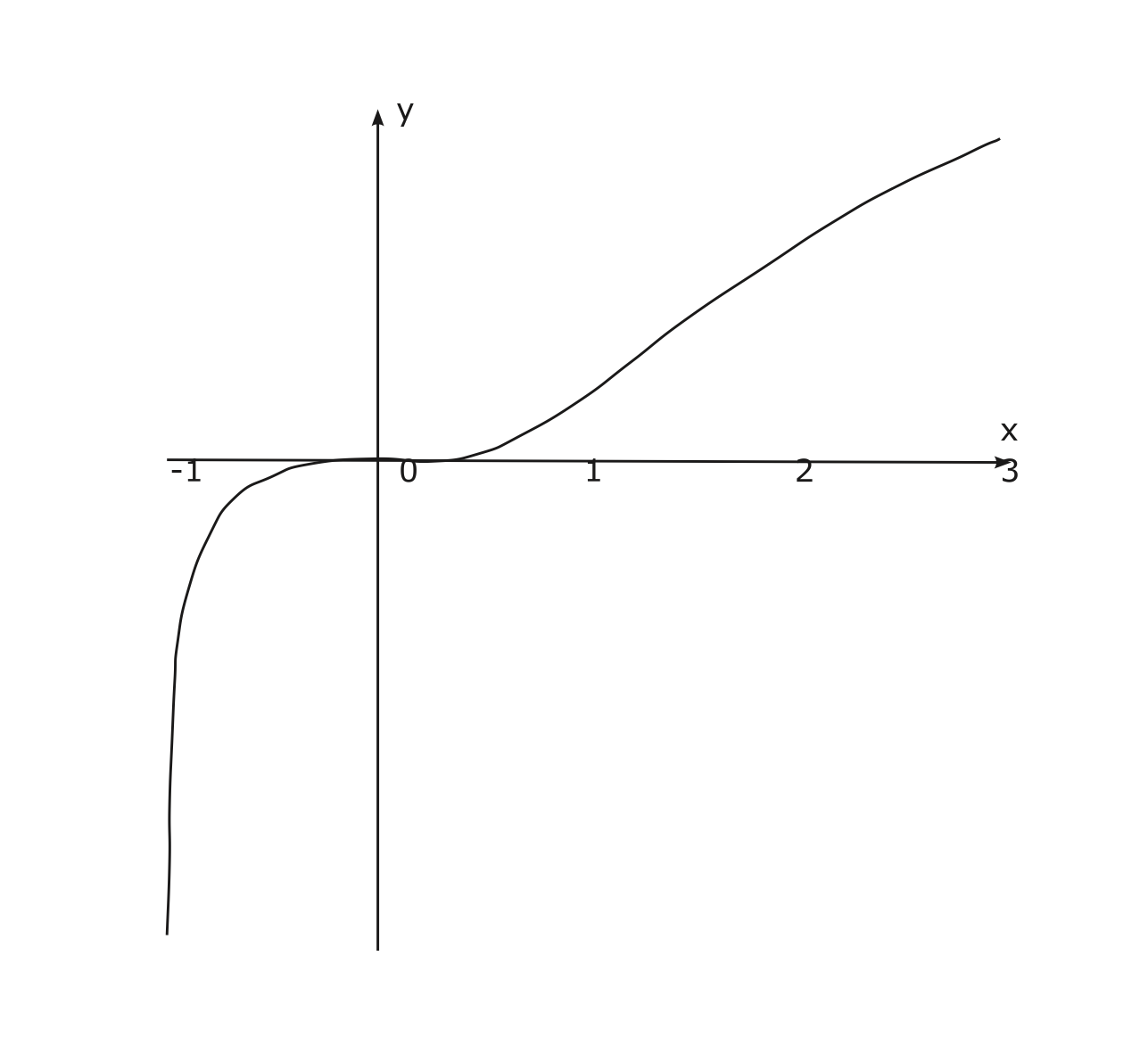
Figure 4.4: กราฟของฟังก์ชัน \(f(x) = \ln(x^3+1)\) บนช่วง \((-1,\infty)\)

ตัวอย่าง 4.15 พิจารณาฟังก์ชัน \(f\) ซึ่งนิยามบนช่วง \((-3,3)\) และหา derivative อันดับสองได้ ฟังก์ชัน
\(f\) มีกราฟดังรูป 4.5

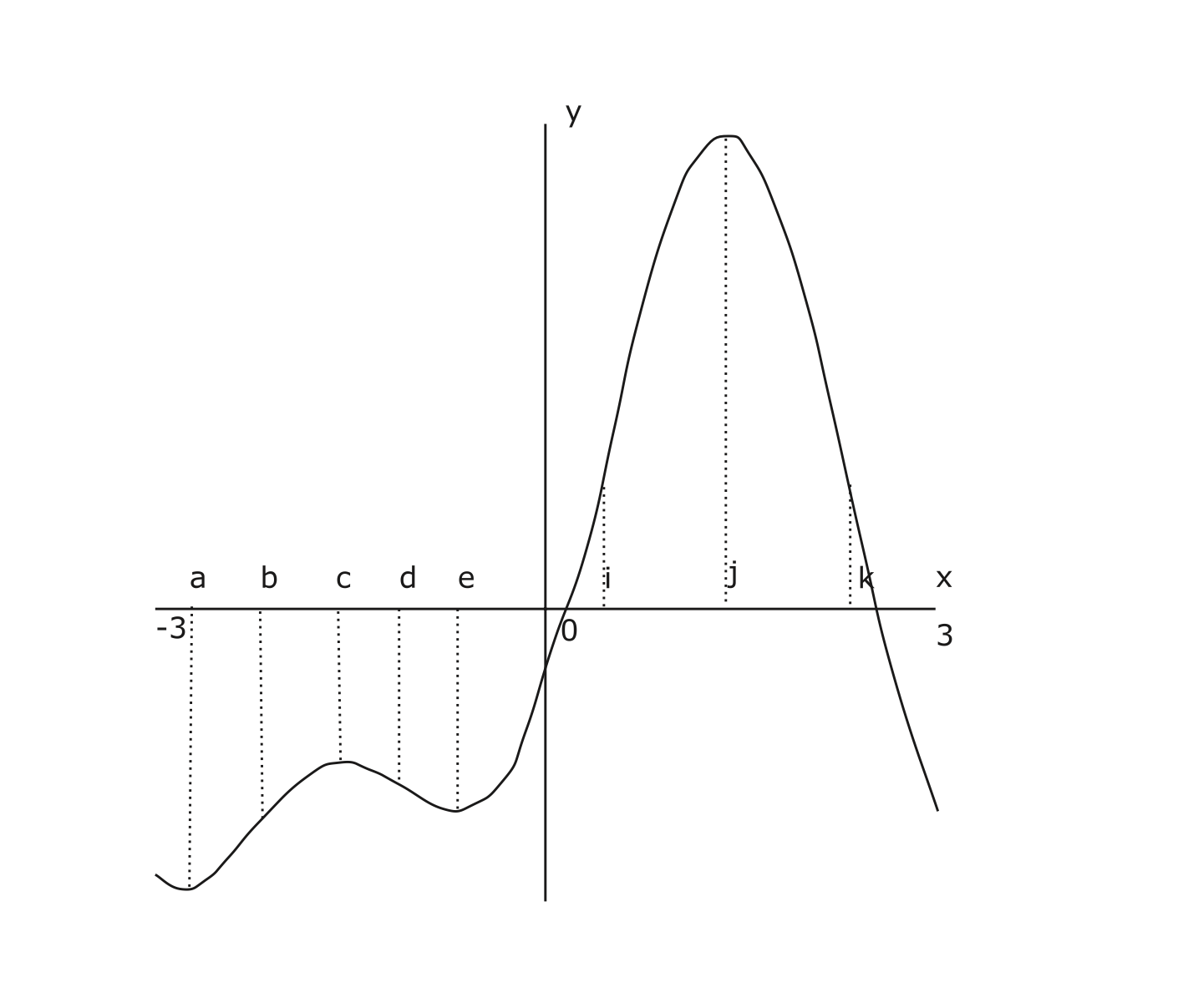
Figure 4.5: กราฟของฟังก์ชัน \(f(x)\) บนช่วง \((-3,3)\)

ที่จุดใดที่ฟังก์ชัน \(f'\) เปลี่ยนเครื่องหมาย และที่จุดใด \(f'\) มี relative extrema

วิธีทำ จากรูป ที่จุดซึ่ง \(f'\) เปลี่ยนเครื่องหมายคือจุด \(x\) ที่ \(f'(x) = 0\) ซึ่ง คือ \(a, c, e\) และ \(j\) ในขณะที่จุดซึ่ง \(f'\) มี relative extrema เป็นจุดซึ่ง \(f''\) เปลี่ยนเครื่องหมาย ในที่นี้คือจุดซึ่ง \(f\) มี inflection point ซึ่งก็คือ \(b, d, i\) และ \(k\)

4.2.1 แบบฝึกหัด

1. พิจารณาฟังก์ชันต่อไปนี้

   1. \(\displaystyle f(x) = x^2-3x+2\)

   2. \(\displaystyle f(x) = \frac{x^2}{x^2+1}\)

   3. \(\displaystyle f(x) = x^{4/3} - x^{1/3}\)

   4. \(\displaystyle f(x) = \ln(1+x^2)\) :::

   ในแต่ละฟังก์ชัน จงหา

   1. \(x\)-intercepts และ \(y\)-intercepts

   2. ช่วงเปิดซึ่ง \(f\) เป็นฟังก์ชันเพิ่ม

   3. ช่วงเปิดซึ่ง \(f\) เป็นฟังก์ชันลด

   4. ช่วงเปิดซึ่ง \(f\) เป็นฟังก์ชัน concave up

   5. ช่วงเปิดซึ่ง \(f\) เป็นฟังก์ชัน concave down

   6. ค่า \(x\) ที่ทำให้ \(f\) มี inflection point :::

2. จงหา relative extrema ของฟังก์ชันต่อไปนี้

   1. \(\displaystyle f(x) = x^3+5x-2\)

   2. \(\displaystyle f(x) = x(x-2)^2\)

   3. \(\displaystyle f(x) = \frac{x}{x-1}\)

   4. \(\displaystyle f(x) = |x^2-1|\) :::

3. จงสเก็ตกราฟของฟังก์ชัน

   1. \(f(x) = x^3-3x+3\)

   2. \(f(x) = -(x+1)x^2(x-1)\)

   3. \(f(x) = e^{1/x}\) :::

4. จงวาดกราฟของฟังก์ชัน \(y=f(x)\) และ \(a<b<c\) จากข้อมูลต่อไปนี้

   1. \(f'(a) = f'(b) = 0\)

   2. \[\begin{equation} \begin{aligned} f'(x) \begin{cases} > 0 &\text{สำหรับ $x<a$} \\ > 0 &\text{สำหรับ $a<x<c$} \\ < 0 &\text{สำหรับ $x>c$} \end{cases} \end{aligned} \end{equation}\]

   3. \(f''(a) = f"'(b) = 0\)

   4. \[\begin{equation} \begin{aligned} f''(x) \begin{cases} < 0 &\text{สำหรับ $x<a$} \\ > 0 &\text{สำหรับ $a<x<b$} \\ < 0 &\text{สำหรับ $x>b$} \end{cases} \end{aligned} \end{equation}\]

5. กำหนดให้ฟังก์ชัน \(f'\) เป็นดังรูป 4.6

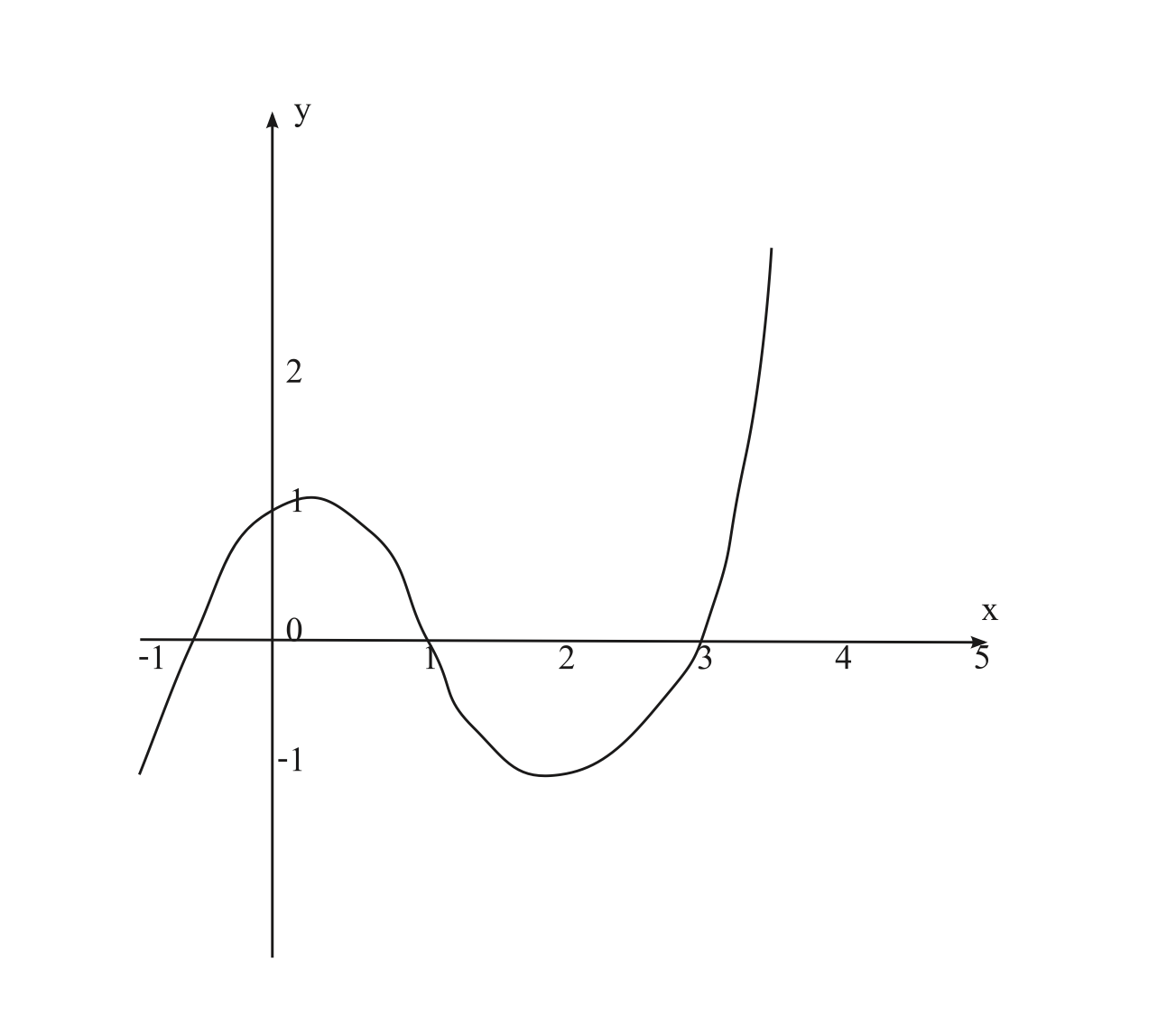
Figure 4.6: กราฟของฟังก์ชัน \(f'(x)\)

จงตอบคำถามต่อไปนี้

1. ช่วงใดที่ \(f\) เป็นฟังก์ชันเพิ่ม

2. ฟังก์ชัน \(f\) มี relative maximum ที่ใด

3. ช่วงใดที่ \(f\) concave up

4. ฟังก์ชัน \(f\) มี inflection point ที่ใด

4.3 การประยุกต์ของ Monotonicity และ Concavity

จากที่ได้ศึกษามาแล้ว ถ้า \(f\) เป็นฟังก์ชันนิยามบนช่วงเปิด \((a,b)\) และ \(x_1\), \(x_2\) เป็นจุดที่อยู่ภายในช่วงดังกล่าว แล้ว

1. \(f\) เป็นฟังก์ชันเพิ่ม ถ้า \(f(x_1)<f(x_2)\) เมื่อ \(x_1<x_2\) หรือ \(f'(x)>0\) สำหรับทุกค่า \(x\) ที่อยู่ในช่วง \((a,b)\)

2. \(f\) เป็นฟังก์ชันลด ถ้า \(f(x_2)<f(x_1)\) เมื่อ \(x_1<x_2\) หรือ \(f'(x)<0\) สำหรับทุกค่า \(x\) ที่อยู่ในช่วง \((a,b)\) นอกจากนี้แล้ว

3. \(f\) มีลักษณะแบบ concave up ในช่วง \((c,d)\) ถ้า \(f'\) เป็นฟังก์ชันเพิ่มในช่วงดังกล่าว หรือ \(f''(x)>0\) สำหรับทุกค่า \(x\) ที่อยู่ในช่วง \((c,d)\)

4. \(f\) มีลักษณะแบบ concave down ในช่วง \((c,d)\) ถ้า \(f'\) เป็นฟังก์ชันลดในช่วงดังกล่าว หรือ \(f''(x)<0\) สำหรับทุกค่า \(x\) ที่อยู่ในช่วง \((c,d)\)

ซึ่งสามารถนำมาประยุกต์ใช้กับปัญหาทางวิทยาศาสตร์ชีวภาพ ดังตัวอย่างต่อไปนี้

ตัวอย่าง 4.16 อัตราการเจริญเติบโตของพืชขึ้นอยู่กับธาตุอาหารที่ได้รับซึ่ง Monod ได้อธิบายไว้ดังสมการ \[f(R)=\frac{aR}{K+R}, \quad R \ge 0\] โดยที่ \(f(R)\) เป็นอัตราการเจริญเติบโต, \(R\) เป็นระดับธาตุอาหาร, \(a\) และ \(K\) เป็นค่าบวกใดๆ ขึ้นอยู่กับชนิดของพืช อยากทราบว่าอัตราการเจริญเติบโตของพืชจะเพิ่มขึ้น หรือลดลงเมื่อไหร่

กำหนดให้ \(R\) เป็นระดับธาตุอาหาร \(f(R)\) เป็นอัตราการเจริญเติบโต เนื่องจาก \[f(R)=\frac{aR}{K+R}, \quad R \ge 0\] จะได้ \[f'(R)=\frac{aK}{(K+R)^2}>0\] เพราะ \(a>0\), \(K>0\) ดังนั้น อัตราการเจริญเติบโตของพืชจะเพิ่มขึ้นและจะไม่มีวันลดลง

ตัวอย่าง 4.17 จากตัวอย่างที่แล้ว เราทราบว่า อัตราการเจริญเติบโตของพืชเป็นฟังก์ชันเพิ่ม อยากทราบว่าอัตราการเพิ่มของอัตราการเจริญเติบโตของพืชจะเป็นอย่างไร

เนื่องจาก \(\displaystyle f(R)=\frac{aR}{K+R}, \quad R \ge 0\) จะได้ \(\displaystyle f'(R)=\frac{aK}{(K+R)^2}>0\) นั่นคือ อัตราการเจริญเติบโตของพืชเป็นฟังก์ชันเพิ่ม โจทย์อยากทราบว่าอัตราการเจริญเติบโตของพืชที่เพิ่มขึ้นนี้จะเพิ่มขึ้นด้วยอัตราเท่าไร นั่นคือการหาอนุพันธ์ของ \(f'(R)\) จะได้ \(\displaystyle f''(R)=\frac{-2aK}{(K+R)^3}<0\) หมายความว่าอัตราการเจริญเติบโตของพืชนั้นเพิ่มขึ้น แต่อัตราการเพิ่มขึ้นนั้นจะลดลง ดังรูป 4.7

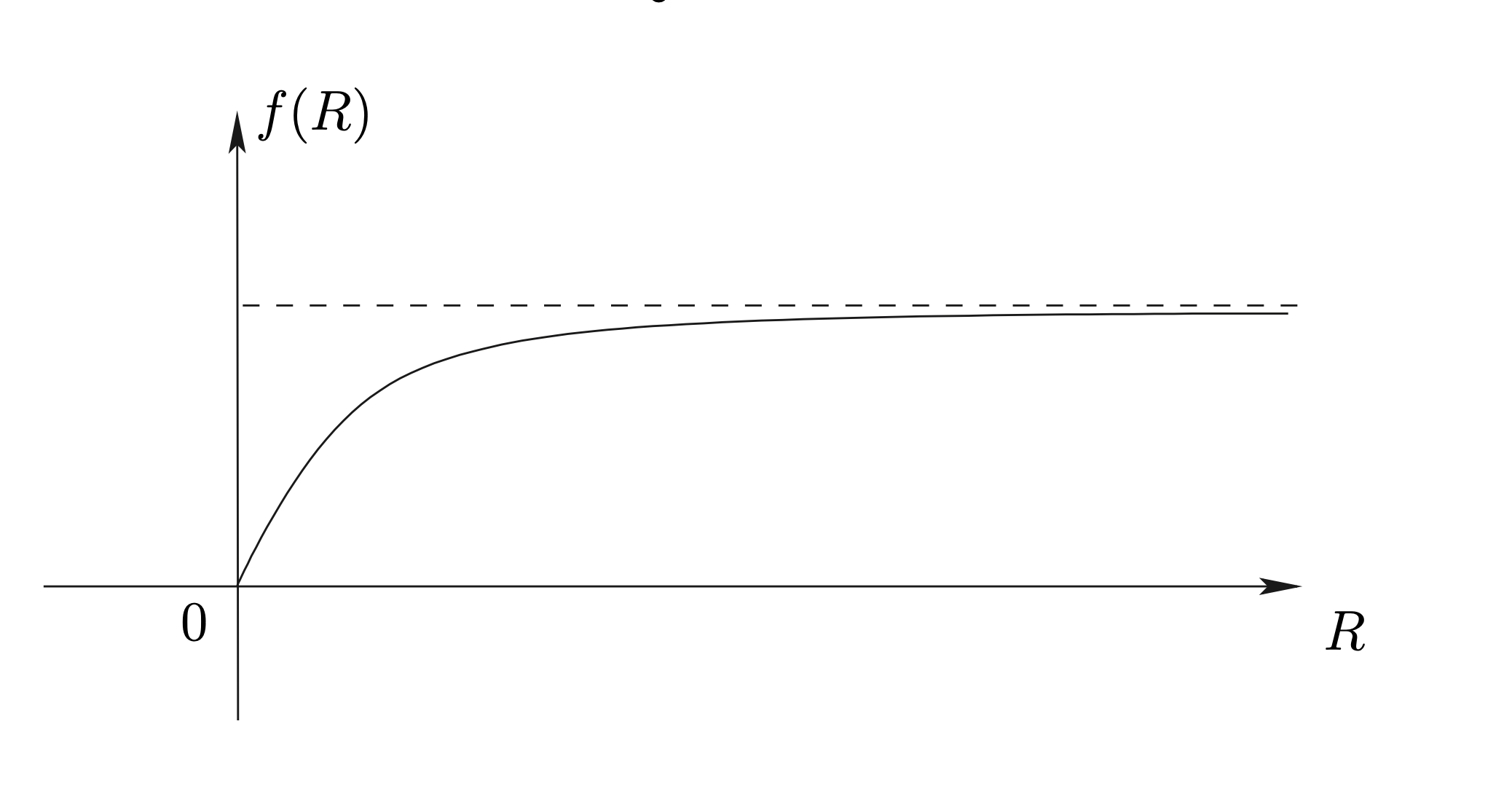
Figure 4.7: กราฟของฟังก์ชัน \(f(R)=\frac{aR}{K+R}\)

ตัวอย่าง 4.18 อัตราการเจริญเติบโตของประชากรสามารถอธิบายได้ด้วยสมการ logistic \[f(N)=rN(1- \frac{N}{K})\] เมื่อ \(N\) เป็นจำนวนประชากร, \(r\) และ \(K\) เป็นค่าบวก อยากทราบว่าอัตราการเจริญเติบโตของประชากรจะเพิ่มขึ้น หรือลดลงอย่างไร

โจทย์ต้องการทราบว่า \(f(N)\) จะเพิ่มขึ้นหรือลดลงอย่างไร นั่นคือ \(f'(N)>0\) หรือ \(f'(N)<0\) เมื่อ \(N\) อยู่ในช่วงใด เนื่องจากอนุพันธ์ใช้ศึกษาการเปลี่ยนแปลงแบบค่อยเป็นค่อยไป ดังนั้น \(f'(N)\) จะเปลี่ยนจากค่าลบเป็นค่าบวก ย่อมต้องผ่านค่าศูนย์ก่อน การหาค่า \(N^*\) ที่ทำให้ \(f(N^*)=0\) ย่อมเป็นหนทางหนึ่งที่สามารถใช้พิจารณาช่วงที่ทำให้ \(f'(N)>0\) และ \(f'(N)<0\) ได้ จาก \(\displaystyle f(N)=rN(1- \frac{N}{K})\) จะได้ \[f'(N)=r- \frac{2rN}{K}\] ซึ่ง \(f'(N)=0\) เมื่อ \(N = \frac{K}{2}\)

ถ้า \(\displaystyle N> \frac{K}{2}\) \(f'(N)<0\) และถ้า \(\displaystyle N< \frac{K}{2}\) \(f'(N)>0\) ดังนั้น อัตราการเจริญเติบโตของประชากรจะเพิ่มขึ้น เมื่อ \(\displaystyle N< \frac{K}{2}\) และจะลดลง เมื่อ \(\displaystyle N> \frac{K}{2}\) แสดงว่าประชากรยิ่งหนาแน่น อัตราการเพิ่มของประชากรก็จะยิ่งลดลง

4.3.1 แบบฝึกหัด

1. จากตัวอย่างที่ 9 จงวาดกราฟของ \(f(N)\) และระบุช่วงที่ทำให้ \(f\) มีลักษณะแบบ concave up และแบบ concave down

2. ค่า \(pH\) ของสารละลายสัมพันธ์กับความเข้มข้นของไฮโดรเจนอิออน, \(H^+\), ดังนี้ \[pH=-log(H^+)\] จงพิจารณาว่าค่า \(pH\) ของสารละลายจะเพิ่มขึ้นหรือลดลงอย่างไร

4.4 การหาค่าเหมาะที่สุด (Optimization)

การหาค่าเหมาะที่สุด คือปัญหาที่ต้องการทราบค่าสูงสุด (absolute maximum) และค่าต่ำสุด (absolute minimum) ดังตัวอย่างต่อไปนี้

ตัวอย่าง 4.19 ผลผลิตของพืชผักสัมพันธ์กับปริมาณไนโตรเจนดังสมการ \(\displaystyle Y(N)= \frac{N}{1+N^2}\) เมื่อ \(Y(N)\) เป็นผลผลิตของพืชผัก และ \(N\) เป็นปริมาณไนโตรเจน \((N \ge 0)\) จงหาปริมาณไนโตรเจนที่ทำให้ได้ผลผลิตของพืชผักมากที่สุด

กำหนดให้ \(N\) เป็นปริมาณไนโตรเจน \(Y(N)\) เป็นผลผลิตของพืชผัก จากความสัมพันธ์ \[Y(N)= \frac{N}{1+N^2}\] หาอนุพันธ์ทั้ง 2 ข้างของสมการ \[Y'(N)= \frac{(1+N^2)-N(2N)}{(1+N^2)^2}= \frac{1-N^2}{(1+N^2)^2}\] กำหนดให้ \(Y'(N)=0\) เพื่อหา relative extrema \(Y'(N)=0\) เมื่อ \(1-N^2=0\) ดังนั้น \(N= \pm 1\)

เราจะพิจารณา \(N\) ในช่วง \(N \ge 0\) ดังนั้น \(N=-1\) จึงอยู่นอกโดเมน จุดที่สนใจจึงเหลือเพียง \(N=1\) โดยพิจารณาเครื่องหมายของ \(Y'(N)\) เราจะได้ว่า \[Y'(N) > 0 \text{ เมื่อ } -1< N <1 \quad Y'(N) < 0 \text{ เมื่อ } N > 1\] เนื่องจาก \(Y(N)\) เปลี่ยนจากฟังก์ชันเพิ่ม เป็นฟังก์ชันลด ที่ \(N=1\) ดังนั้น ที่ \(N=1\) เกิดจากจุดสูงสุดสัมพัทธ์ (relative maximum) โดย \(Y(1)= \frac{1}{2}\)

เนื่องจากเราสนใจ absolute maximum จึงต้องตรวจสอบจุดปลายของโดเมน (\(N \ge 0\) หรือ \(N \in [0,\infty)\)) นั่นคือ \(N=0\) และ \(N \rightarrow \infty\) ด้วย ว่าทำให้ \(Y\) มีค่ามากกว่า \(Y(1)= \frac{1}{2}\) หรือไม่ \[Y(0)=0, \quad \lim_{N \rightarrow \infty} Y(N) =\lim_{N \rightarrow \infty} \frac{N}{1+N^2} = 0\] ดังนั้นที่ \(N=1\) จะเกิดจุดสูงสุดสัมบูรณ์ (absolute maximum) ซึ่งเป็นปริมาณไนโตรเจนที่ทำให้พืชผักมีผลผลิตมากที่สุด คือ \(Y(1)= \frac{1}{2}\) (ดูกราฟ 4.8)

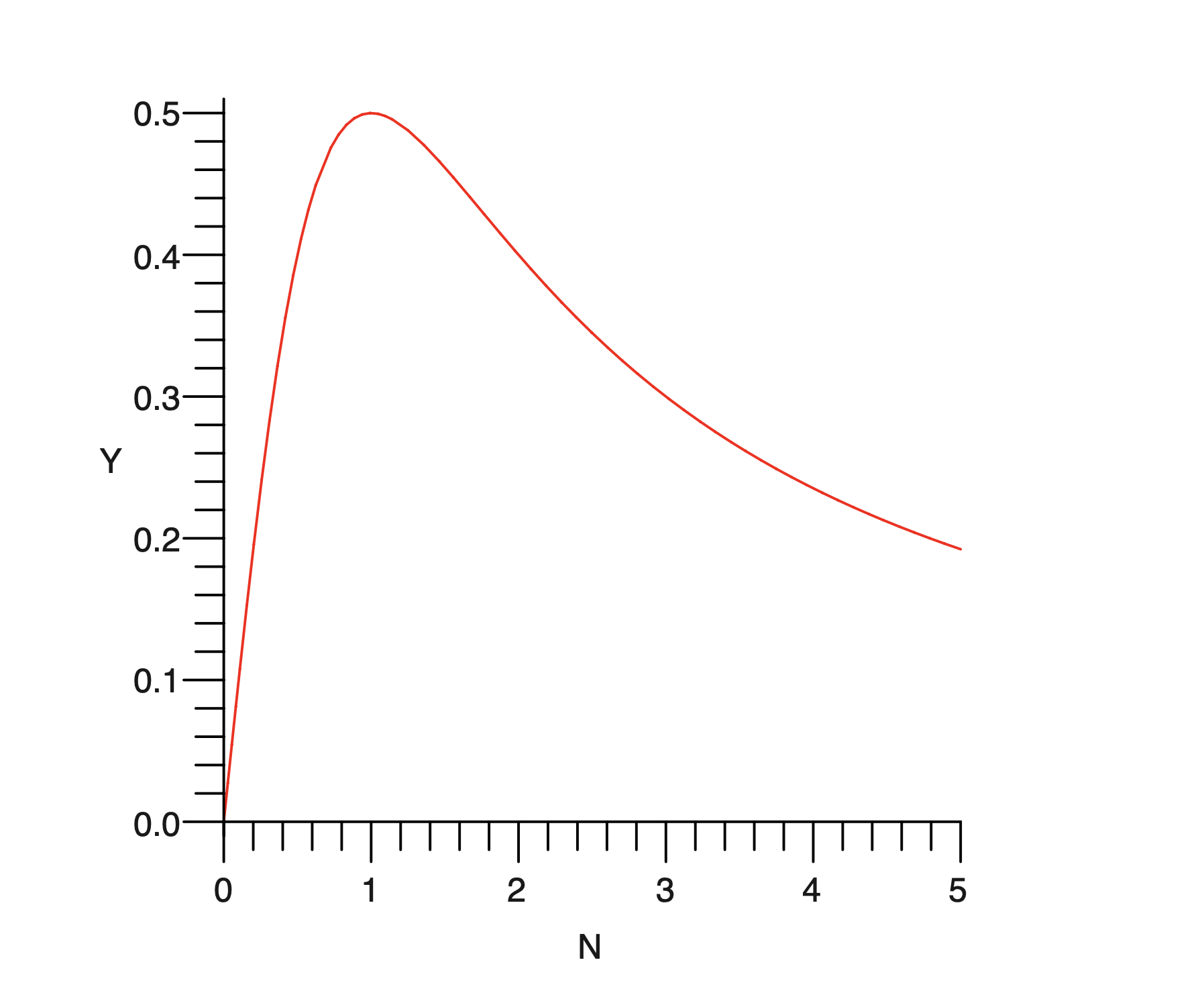
Figure 4.8: กราฟของฟังก์ชัน \(Y(N) = \frac{N}{1 + N^2}\)

ตัวอย่าง 4.20 เรือบรรทุกน้ำมันของบริษัทแห่งหนึ่งอับปางลงบริเวณอ่าวไทย ทำให้น้ำมันไหลรั่วซึมลงสู่ทะเล กระทบต่อระดับออกซิเจนที่ละลายอยู่ในน้ำ และสิ่งมีชีวิตที่อาศัยอยู่ในบริเวณดังกล่าว สมมติว่าระดับออกซิเจนที่ละลายอยู่ในน้ำ หลังเหตุการณ์เรือล่ม มีการเปลี่ยนแปลงดังสมการ \[P(t)=500[1- \frac{4}{t+4} + \frac{16}{(t+4)^2}]\] เมื่อ \(P(t)\) เป็นระดับออกซิเจนที่ละลายอยู่ในน้ำ หลังเหตุการณ์เรือล่มผ่านพ้นไป \(t\) เดือน อยากทราบว่าเมื่อไหร่ออกซิเจนที่ละลายอยู่ในน้ำบริเวณดังกล่าวจะอยู่ในระดับที่ต่ำที่สุด

กำหนดให้ \(t\) เป็นเวลาหลังเหตุการณ์เรือล่ม \(P(t)\) เป็นระดับออกซิเจนที่ละลายอยู่ในน้ำ บริเวณที่เกิดเหตุ

จาก \(P(t)=500[1- \frac{4}{t+4} + \frac{16}{(t+4)^2}]\) หาอนุพันธ์ทั้ง 2 ข้างของสมการ \[\begin{equation} \begin{aligned} P'(t) &= \frac{2000}{(t+4)^2} - \frac{16000}{(t+4)^3} \\ &=\frac{2000(t+4)-16000}{(t+4)^3} \\ &=\frac{2000t-8000}{(t+4)^3} \end{aligned} \end{equation}\]

กำหนดให้ \(\displaystyle P'(t)= \frac{2000t-8000}{(t+4)^3}=0\) จะได้ \(t=4\) เครื่องหมายของ \(P'(t) > 0\) เมื่อ \(t > 4\) และ \(P'(t) ฒ 0\) เมื่อ \(t < 4\) ดังนั้น \(P(t)\) เปลี่ยนจากฟังก์ชันลดเป็นฟังก์ชันเพิ่มที่ \(t=4\) ดังนั้น ที่ \(t=4\) เกิดจุดต่ำสุดสัมพัทธ์ (relative minimum) โดย \(P(4)=375\)

เนื่องจากเราสนใจ absolute minimum จึงต้องตรวจสอบค่า \(P(t)\) ที่จุดปลายของโดเมน \(t\) ด้วย นั่นคือ \(t = 0\) และ \(t \rightarrow \infty\) \(P(0)=500\) และ \(\lim_{t \rightarrow \infty} P(t) = 500\) ดังนั้น ที่ \(t=4\) เกิดจุดต่ำสุดสัมบูรณ์ (absolute minimum) ระดับออกซิเจนที่ละลายอยู่ในน้ำ บริเวณดังกล่าวต่ำสุด หลังเหตุการณ์เรืออับปางผ่านพ้นไป 4 เดือน

ตัวอย่าง 4.21 นักชีววิทยาต้องการออกแบบพื้นที่ทดลองให้เป็นรูปสี่เหลี่ยมมุมฉาก เขามีรั้วยาว 1600 ฟุต เขาจะใช้รั้วนี้อย่างไร จึงจะทำให้ได้พื้นที่ทดลองที่กว้างใหญ่ที่สุด

กำหนดให้

\(x\) เป็นความกว้างของพื้นที่ทดลอง
\(y\) เป็นความยาวของพื้นที่ทดลอง
\(A\) เป็นพื้นที่ของพื้นที่ทดลอง
\(P\) เป็นความยาวรอบรูปของพื้นที่ทดลอง

เนื่องจาก \(A=xy\) และ \(P=2x+2y\) จากโจทย์ \(P=2x+2y=1600\) ดังนั้น \(x+y=800\) หรือ \(y=800-x\) แทน \(y\) ลงใน \(A=xy\) จะได้ \[\begin{equation} \begin{aligned} A(x) &=x(800-x), \quad 0 \le x \le 800 \\ &=800x-x^2 \end{aligned} \end{equation}\] โจทย์ต้องการหาพื้นที่กว้างใหญ่ที่สุด เราจึงต้องหาอนุพันธ์ทั้ง 2 ข้าง \[A'(x)=800-2x\] กำหนดให้ \(A'(x)=800-2x=0\) จะได้ \(x=400\) และ \(A(400)=1600\) ตามลำดับ ทดสอบโดยใช้อนุพันธ์อันดับสอง \(A''(x)=-2<0\) พบว่า \(x=400\) ทำให้เกิดจุดสูงสุดสัมบูรณ์ เพราะ \(A(x)\) มีลักษณะแบบ concave down ดังนั้นนักชีววิทยาควรกั้นรั้วเป็นรูปสี่เหลี่ยมจัตุรัสกว้าง 400 ฟุต จึงจะได้พื้นที่ทดลองที่กว้างใหญ่ที่สุด

1. วาดภาพและกำหนดตัวแปรต่างๆ เช่น \(x\), \(y\) เป็นต้น

2. หาสูตรหรือสมการของปริมาณที่ต้องการหาค่าสูงสุดหรือค่าต่ำสุด

3. ใช้เงื่อนไขที่โจทย์ระบุให้ในการตัดทอนตัวแปร เพื่อทำให้สมการในขั้นตอนที่ 2 อยู่ในรูปฟังก์ชันที่ขึ้นอยู่กับตัวแปรเพียงตัวเดียว

4. หาช่วงที่เป็นไปได้ของตัวแปร โดยให้สอดคล้องกับความหมายของโจทย์

5. ใช้เทคนิคการหาค่าสูงสุด/ต่ำสุดสัมพัทธ์ ไม่ว่าจะเป็นทดสอบด้วยอนุพันธ์อันดับหนึ่ง หรือทดสอบด้วยอนุพันธ์อันดับสอง

6. ตรวจสอบจุดปลายของโดเมนของตัวแปร เพื่อยืนยันการเกิดค่าสูงสุด/ต่ำสุดสัมบูรณ์

4.4.1 แบบฝึกหัด

1. อัตราการเปลี่ยนแปลงของการสังเคราะห์แสงขึ้นกับความเข้มของแสง \(x\), ซึ่งสอดคล้องกับสมการ \(R(x)=270x-90x^2\) จงหาความเข้มของแสง ที่ทำให้อัตราการเปลี่ยนแปลงของการสังเคราะห์แสงมากที่สุด

2. การตอบสนองต่อยาชนิดหนึ่งขึ้นกับปริมาณของยา, \(x\), ดังสมการ \(S=1000x-x^2\) จงหาปริมาณยาที่ทำให้มีการตอบสนองต่อยาชนิดนี้มากที่สุด

3. นักวิจัยพบว่าขณะไอ ปริมาณอากาศที่ไหลผ่านทางหลอดลมสัมพันธ์กับสมการ \(F=SA\) เมื่อ \(S\) คือความเร็วของอากาศ และ \(A\) คือพื้นที่ตัดขวางของหลอดลม ดังรูป 4.9 ถ้าความเร็วของอากาศมีสูตรเป็น \(S=c-r\) โดย \(r\) คือรัศมีของหลอดลมขณะไอ และ \(c\) คือรัศมีของหลอดลมในสภาวะปกติ จงหารัศมีที่ทำให้ปริมาณอากาศที่ไหลผ่านหลอดลมมีมากที่สุด ขณะที่ไอ

4. เภสัชกรต้องการสร้างกล่องไร้ฝาอย่างง่ายเพื่อขนย้ายยา เขามีกระดาษแข็งกว้าง 16 นิ้ว ยาว 30 นิ้ว เขาตั้งใจจะตัดมุมของกระดาษแข็งทั้ง 4 ออก ตามรูป 4.10 แล้วทำการพับตามรอยปะและเชื่อมรอยต่อด้วยเทปกาว จงหาความยาว \(x\) ที่ตัดตามมุม เพื่อให้ได้กล่องที่มีปริมาตรมากที่สุด

5. คราวนี้นักชีววิทยาคนเดิม ต้องการพื้นที่ทดลองแบบสี่เหลี่ยมมุมฉากขนาด 320 ตารางเมตร ด้านที่ขนานกันคู่หนึ่งใช้รั้วราคา 100 บาทต่อเมตร ส่วนด้านคู่ที่เหลือใช้รั้วราคา 200 บาทต่อเมตร จงหาความกว้างและความยาวของพื้นที่ทดลองแห่งนี้ เมื่อใช้งบประมาณน้อยที่สุด

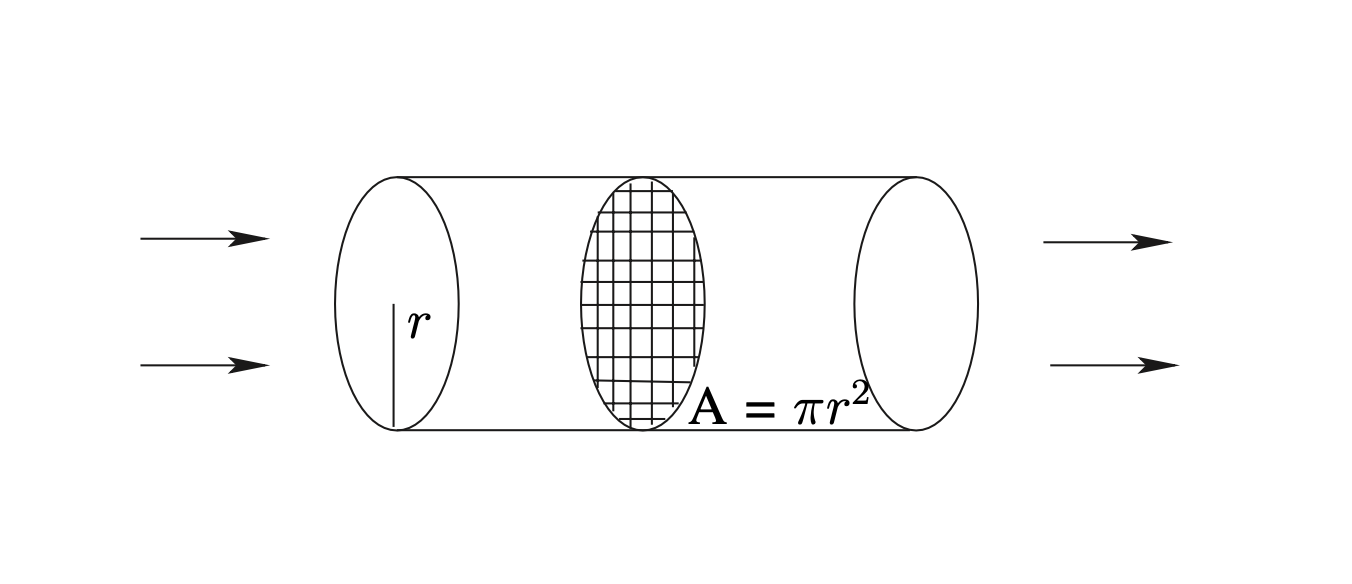
Figure 4.9: การไหลเวียนของอากาศในหลอดลม

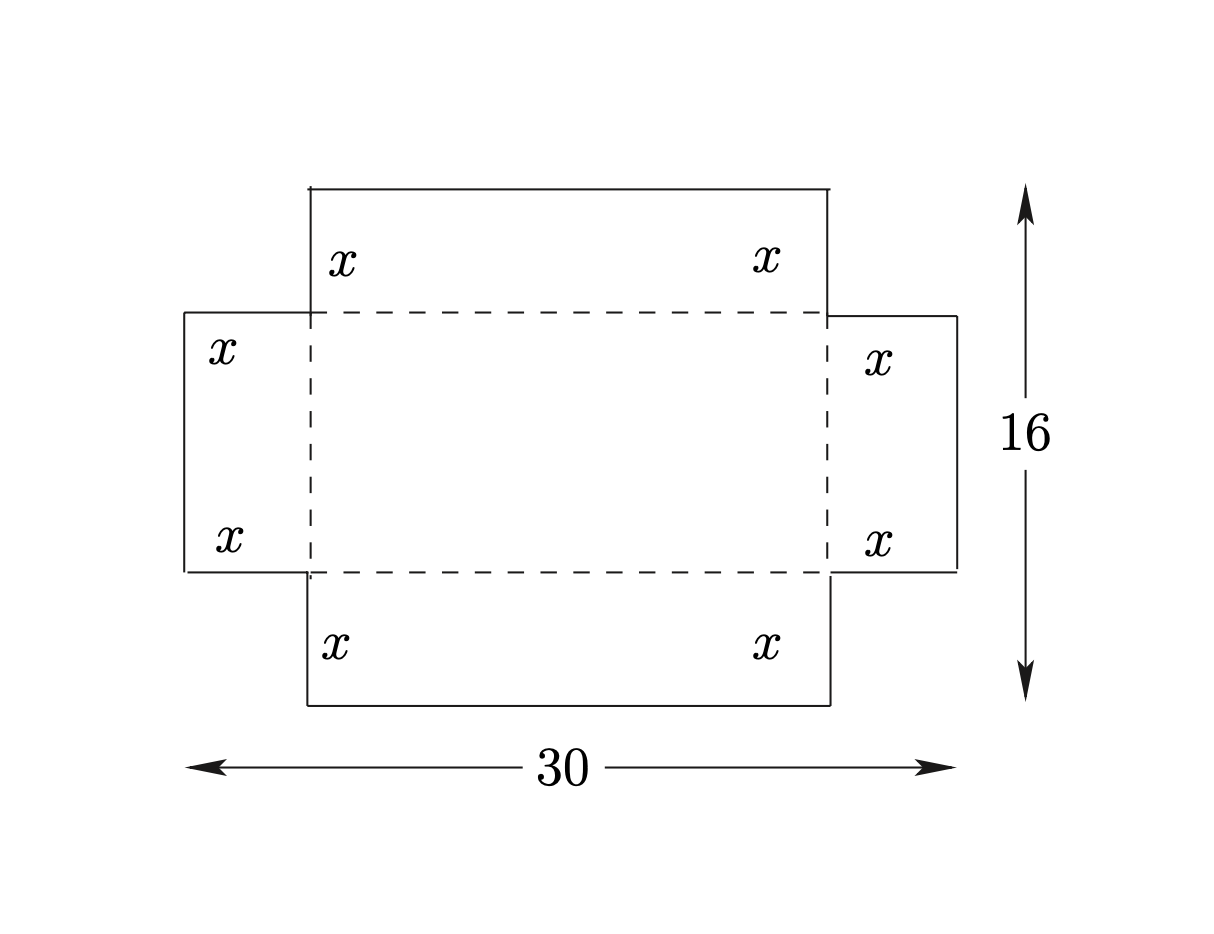
Figure 4.10: กล่องไร้ฝาสำหรับขนส่งยา

4.5 รูปแบบไม่กำหนด (Indeterminate form) และกฎของโลปิตาล (L’Hopital Rule)

นิยาม 4.6 ถ้า \(\mathop {\lim }\limits_{x\to a} f(x)=0\) และ \(\displaystyle \mathop {\lim }\limits_{x\to a} g(x)=0\) เราจะกล่าวว่า \(\displaystyle \mathop {\lim }\limits_{x\to a} \frac{f(x)}{g(x)}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) อาจแทน \(x\to a\) ด้วย \(x\to a^+\) , \(x\to a^-\) , \(x\to \infty\) , \(x\to -\infty\)

ในการหาค่าลิมิตของรูปแบบไม่กำหนดแบบ \(\displaystyle \frac{0}{0}\) นั้น เราจะนำกฎของโลปิตาลมาประยุกต์ใช้

ทฤษฎี 4.5 (กฎของโลปิตาล)

1. ถ้า \(\mathop {\lim }\limits_{x\to a} f(x)=0\) และ \(\mathop {\lim }\limits_{x\to a} g(x)=0\) แล้ว \(\displaystyle \mathop {\lim }\limits_{x\to a} \frac{f(x)}{g(x)}\) จะอยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) และได้ว่า \(\displaystyle \mathop {\lim }\limits_{x\to a} \frac{f(x)}{g(x)}=\mathop {\lim }\limits_{x\to a} \frac{{f}'(x)}{{g}'(x)}\)
   

2. ถ้า \(\mathop {\lim }\limits_{x\to a} f(x)=\infty\) และ \(\mathop {\lim }\limits_{x\to a} g(x)=\infty\) แล้ว \(\displaystyle \mathop {\lim }\limits_{x\to a} \frac{f(x)}{g(x)}\) จะอยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{\infty }{\infty }\) และได้ว่า \(\displaystyle \mathop {\lim }\limits_{x\to a} \frac{f(x)}{g(x)}=\mathop {\lim }\limits_{x\to a} \frac{{f}'(x)}{{g}'(x)}\)

ตัวอย่าง 4.22 จงหาค่าของ \(\displaystyle \mathop {\lim }\limits_{x\to 5} \frac{\sqrt {x-1} -2}{x^2-25}\)

วิธีทำ เพราะว่า \(\displaystyle \mathop {\lim }\limits_{x\to 5} \frac{\sqrt {x-1} -2}{x^2-25}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) \[\displaystyle \mathop {\lim }\limits_{x\to 5} \frac{\sqrt {x-1} -2}{x^2-25}=\mathop {\lim }\limits_{x\to 5} \frac{1}{(2\sqrt {x-1} )(2x)}=\frac{1}{40}\]

กฎของโลปิตาลยังคงเป็นจริงในกรณีที่ \(x\to a^+\) , \(x\to a^-\) , \(x\to \infty\) , \(x\to -\infty\)

ตัวอย่าง 4.23 จงหาค่าของ \(\displaystyle \mathop {\lim }\limits_{x\to \infty } \frac{\ln x}{\sqrt x }\)

วิธีทำ เพราะว่า \(\displaystyle \mathop {\lim }\limits_{x\to \infty } \frac{\ln x}{\sqrt x }\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{\infty }{\infty }\) \[\displaystyle \mathop {\lim }\limits_{x\to \infty } \frac{\ln x}{\sqrt x }=\mathop {\lim }\limits_{x\to \infty } \frac{1/x}{1/2\sqrt x }=\mathop {\lim }\limits_{x\to \infty } \frac{2}{\sqrt x }=0\]

กฎของโลปิตาลใช้กับลิมิตที่อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) หรือ \(\displaystyle \frac{\infty }{\infty }\) เท่านั้น หากลิมิตไม่ได้อยู่ในรูปแบบดังกล่าว เราจะต้องจัดให้อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) หรือ \(\displaystyle \frac{\infty }{\infty }\) เสียก่อนแล้วจึงนำกฎของโลปิตาลมาใช้

4.5.1 การหาลิมิตที่อยู่ในรูปแบบไม่กำหนด \(0\cdot \infty\) หรือ \(\infty -\infty\)

การหาลิมิตในรูปแบบไม่กำหนด \(0\cdot \infty\) หรือ \(\infty -\infty\) สามารถทำได้โดยจัดให้ลิมิตอยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) หรือ \(\displaystyle \frac{\infty }{\infty }\) ก่อนแล้วจึงนำกฎของโลปิตาลมาใช้ ดังตัวอย่างต่อไปนี้

ตัวอย่าง 4.24 จงหาค่าของ \(\mathop {\lim }\limits_{x\to 0^+} x\ln x\)

วิธีทำ เพราะว่า \(\displaystyle \mathop {\lim }\limits_{x\to 0^+} x\ln x=\mathop {\lim }\limits_{x\to 0^+} \frac{\ln x}{1/x}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{\infty }{\infty }\) \[\displaystyle \mathop {\lim }\limits_{x\to 0^+} \frac{\ln x}{1/x}=\mathop {\lim }\limits_{x\to 0^+} \frac{1/x}{-1/x^2}=\mathop {\lim }\limits_{x\to 0^+} (-x)=0\]

ตัวอย่าง 4.25 จงหาค่าของ \(\displaystyle \mathop {\lim }\limits_{x\to 1} (\frac{1}{x-1}-\frac{1}{\ln x})\)

วิธีทำ เพราะว่า \(\displaystyle \mathop {\lim }\limits_{x\to 1} (\frac{1}{x-1}-\frac{1}{\ln x})=\mathop {\lim }\limits_{x\to 1} \frac{\ln x-x+1}{(x-1)\ln x}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\)

\[\displaystyle \mathop {\lim }\limits_{x\to 1} \frac{\ln x-x+1}{(x-1)\ln x}=\mathop {\lim }\limits_{x\to 1} \frac{(\frac{1}{x}-1)}{(\frac{x-1}{x})+\ln x}=\mathop {\lim }\limits_{x\to 1} \frac{1-x}{x-1+x\ln x}\] ซึ่งยังอยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) \[\displaystyle \mathop {\lim }\limits_{x\to 1} \frac{1-x}{x-1+x\ln x}=\mathop {\lim }\limits_{x\to 1} \frac{-1}{1+1+\ln x}=\frac{-1}{2}\] ดังนั้น \(\displaystyle \mathop {\lim }\limits_{x\to 1} (\frac{1}{x-1}-\frac{1}{\ln x})=-\frac{1}{2}\)

4.5.2 การหาลิมิตที่อยู่ในรูปแบบไม่กำหนด \(0^{0}, 1^{\infty}, \infty^0\)

ในการหาค่าลิมิตทั้ง 3 แบบนี้ เราสามารถจัดให้ลิมิตอยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\) หรือ \(\displaystyle \frac{\infty }{\infty }\) โดยอาศัยฟังก์ชันลอการิทึมเข้าช่วย แล้วจึงนำกฎของโลปิตาลมาใช้ ดังตัวอย่างต่อไปนี้

ตัวอย่าง 4.26 จงหาค่าของ \(\mathop {\lim }\limits_{x\to 0^+} x^x\)

วิธีทำ ให้ \(y=x^x\) ดังนั้น \(\ln y=x\ln x\)

\(\displaystyle \mathop {\lim }\limits_{x\to 0^+} \ln y=\mathop {\lim }\limits_{x\to 0^+} x\ln x=\mathop {\lim }\limits_{x\to 0^+} \frac{\ln x}{1/x}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{\infty }{\infty }\)

\(\displaystyle \mathop {\lim }\limits_{x\to 0^+} \frac{\ln x}{1/x}=\mathop {\lim }\limits_{x\to 0^+} \frac{1/x}{-1/x^2}=\mathop {\lim }\limits_{x\to 0^+} (-x)=0\)

ดังนั้น \(\mathop {\lim }\limits_{x\to 0^+} \ln y=0\)

เพราะว่า \(\mathop {\lim }\limits_{x\to 0^+} \ln y=\ln (\mathop {\lim }\limits_{x\to 0^+} y)\) ดังนั้น \(\ln (\mathop {\lim }\limits_{x\to 0^+} y)=0\)

นั่นคือ \(\mathop {\lim }\limits_{x\to 0^+} y=e^0=1\)

หรือ \(\mathop {\lim }\limits_{x\to 0^+} x^x=1\)

ตัวอย่าง 4.27 จงหาค่าของ \(\mathop {\lim }\limits_{x\to 1} x^{1/(x-1)}\)

วิธีทำ ให้ \(y=x^{1/(x-1)}\) ดังนั้น \(\displaystyle \ln y=\frac{\ln x}{x-1}\)

และ \(\displaystyle \mathop {\lim }\limits_{x\to 1} \frac{\ln x}{x-1}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{0}{0}\)

\(\displaystyle \mathop {\lim }\limits_{x\to 1} \ln y=\mathop {\lim }\limits_{x\to 1} \frac{\ln x}{x-1}=\mathop {\lim }\limits_{x\to 1} \frac{1}{x}=1\)

ดังนั้น \(\mathop {\lim }\limits_{x\to 1} \ln y=1\)

เพราะว่า \(\mathop {\lim }\limits_{x\to 1} \ln y=\ln (\mathop {\lim }\limits_{x\to 1} y)\) ดังนั้น \(\ln (\mathop {\lim }\limits_{x\to 1} y)=1\)

นั่นคือ \(\mathop {\lim }\limits_{x\to 1} y=e^1=e\)

หรือ \(\mathop {\lim }\limits_{x\to 1} x^{1/(x-1)}=e\)

ตัวอย่าง 4.28 จงหาค่าของ \(\mathop {\lim }\limits_{x\to \infty } x^{1/x}\)

วิธีทำ ให้ \(y=x^{1/x}\) ดังนั้น \(\displaystyle \ln y=\frac{\ln x}{x}\)

และ \(\displaystyle \mathop {\lim }\limits_{x\to \infty } \frac{\ln x}{x}\) อยู่ในรูปแบบไม่กำหนด \(\displaystyle \frac{\infty }{\infty }\)

\(\displaystyle \mathop {\lim }\limits_{x\to \infty } \ln y=\mathop {\lim }\limits_{x\to \infty } \frac{\ln x}{x}=\mathop {\lim }\limits_{x\to \infty } \frac{1/x}{1}=0\)

ดังนั้น \(\mathop {\lim }\limits_{x\to \infty } \ln y=0\)

เพราะว่า \(\mathop {\lim }\limits_{x\to \infty } \ln y=\ln (\mathop {\lim }\limits_{x\to \infty } y)\) ดังนั้น \(\ln (\mathop {\lim }\limits_{x\to \infty } y)=0\)

นั่นคือ \(\mathop {\lim }\limits_{x\to \infty } y=e^0=1\)

หรือ \(\mathop {\lim }\limits_{x\to \infty } x^{1/x}=1\)