บทที่ 2 ลิมิต (Limits)

อาจกล่าวได้ว่า วิชาแคลคูลัส ถือกำเนิดขึ้นมาจากความพยายามในการแก้ปัญหาทางเรขาคณิตบนระนาบ 2 ปัญหาหลักๆ คือ

การหาเส้นตรงที่สัมผัสเส้นโค้งที่กำหนดให้

กำหนดฟังก์ชัน (function) $f$ และกำหนดจุด $P(x_{0},y_{0})$ บนกราฟ $y = f(x)$ จงหาสมการของเส้นตรงที่สัมผัสกราฟ $y = f(x)$ ที่จุด $P$
การหาพื้นที่ของบริเวณที่กำหนดให้

กำหนด function $f$ และช่วง $[a,b]$ ในโดเมนของ $f$ จงหาพื้นที่ที่ถูกปิดล้อมด้วยแกน $X$ และกราฟ $y = f(x)$ สำหรับ $x \in [a,b]$

แนวความคิดในการแก้ปัญหาทั้งสอง นำไปสู่การศึกษาเรื่อง ลิมิต (Limits) ซึ่งเป็นพื้นฐานของวิชาแคลคูลัสนั่นเอง

แต่ในปัจจุบันเราพบว่าวิชาแคลคูลัสมีประโยชน์ในการช่วยแก้ปัญหาในสาขาวิชาต่าง ๆ มากมาย เช่น เราจะพบในการศึกษาวิชานี้ว่า แคลคูลัสมีบทบาทในการแก้ปัญหาต่อไปนี้

โดยทั่วไป ยาชนิดฉีดจะต้องใช้เวลาระยะหนึ่งหลังจากฉีดเข้าสู่ร่างกาย ในการที่จะไหลเวียนในกระแสโลหิต จนกระทั่งมีความเข้มข้นสูงสุด สมมุติว่า ยาฉีดชนิดหนึ่งหลังจากฉีดเข้าสู่ร่างกายนาน $t$ ชั่วโมง จะมีความเข้มข้นเป็น $C(t) = 0.15(e^{-0.18t}-e^{-1.2t})$ มิลลิกรัมต่อมิลลิลิตร จงหาว่า นานเท่าใดหลังจากฉีดยา จึงจะมีความเข้มข้นของยา ในกระแสโลหิตสูงที่สุด
เราอาจประมาณได้อย่างมีเหตุผลว่า artery มีรูปร่างที่เป็นผลมาจากการหมุนรอบแกน ของเส้นโค้งในระนาบ โดยในสภาวะนิ่ง รัศมีของ artery มีค่าคงที่เท่ากับ 1 หน่วย (รูปทรงกระบอก) แต่ในขณะที่หัวใจสูบฉีดโลหิตผ่าน artery artery จะพองตัวออก ทำให้รัศมีเปลี่ยนไปตามสมการ $R(x) = 1+0.4x-0.04x^{2}$ หน่วย เมื่อ $0 \leq x\leq 10$ เป็นตำแหน่งบนแนวยาวของ artery จงหาว่า ปริมาณโลหิตที่อยู่ใน artery ขณะที่หัวใจสูบฉีดโลหิตผ่านเข้ามาเป็นกี่เท่าของความจุโลหิตในสภาวะนิ่ง
ความก้าวหน้าในทางการแพทย์ และเทคโนโลยีปัจจุบัน ทำให้มีการประดิษฐ์อุปกรณ์ช่วยในการรักษาโรคเบาหวานชิ้นหนึ่งขึ้น อุปกรณ์นี้มีลักษณะเป็นแคปซูล ซึ่งเมื่อฝังอุปกรณ์นี้ภายในร่างกายแล้ว มันจะหลั่งสารอินซูลินที่บรรจุอยู่ภายใน ออกสู่กระแสโลหิต โดยมีอัตราการหลั่งเป็น $f\left( t\right) =0.5te^{-0.09t}$ ลูกบาศก์เซนติเมตรต่อวัน เมื่อ t คือ เวลาเป็นวัน นับจากอุปกรณ์เริ่มทำงาน จงหาว่า แพทย์จะต้องสั่งให้บรรจุอินซูลินในแคปซูลเป็นปริมาณเท่าใด เพื่อให้อุปกรณ์นี้สามารถให้อินซูลินแก่ผู้ป่วยได้นาน 3 เดือน
การหาเส้นตรงที่สัมผัสเส้นโค้ง $y = f(x)$ ณ จุด $P_{0}(x_{0},y_{0})$

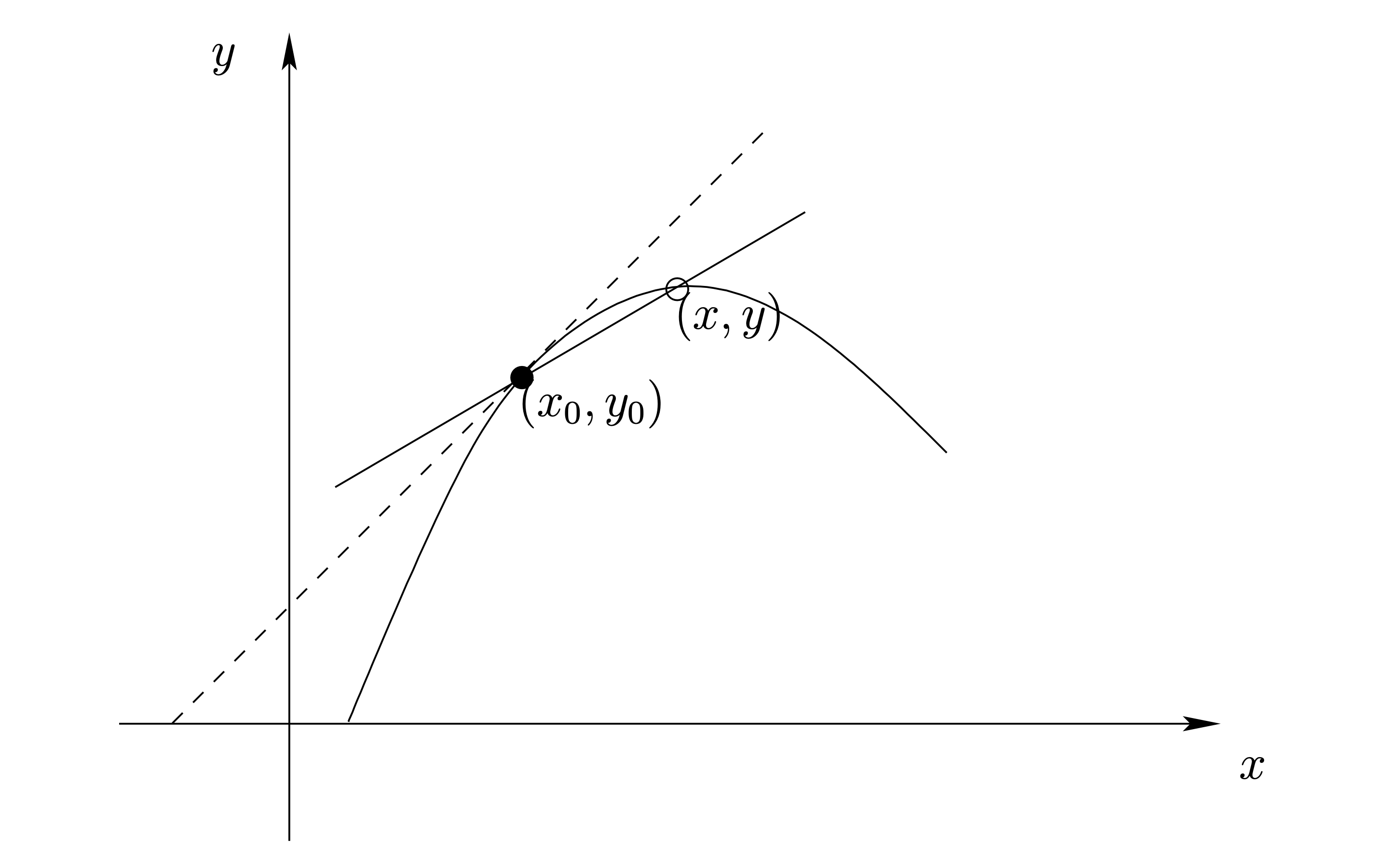
Figure 2.1: การหาเส้นตรงที่สัมผัสเส้นโค้ง

ขั้นตอนสรุปการหาเส้นตรงที่สัมผัสเส้นโค้ง 2.1

เลือกจุดอื่นบนกราฟ เรียกจุดนี้ว่า $P(x,y)$
ลากเส้นผ่าน $PP_{0}$
ทำซ้ำโดยเลือกจุด P ให้ใกล้ $P_{0}$ มากขึ้น
เส้น $PP_{0}$ ที่ได้จะ “เข้าใกล้” เส้นสัมผัสมากขึ้นทุกที

การหาพื้นที่ “ใต้กราฟ” ระหว่าง x = a กับ x = b

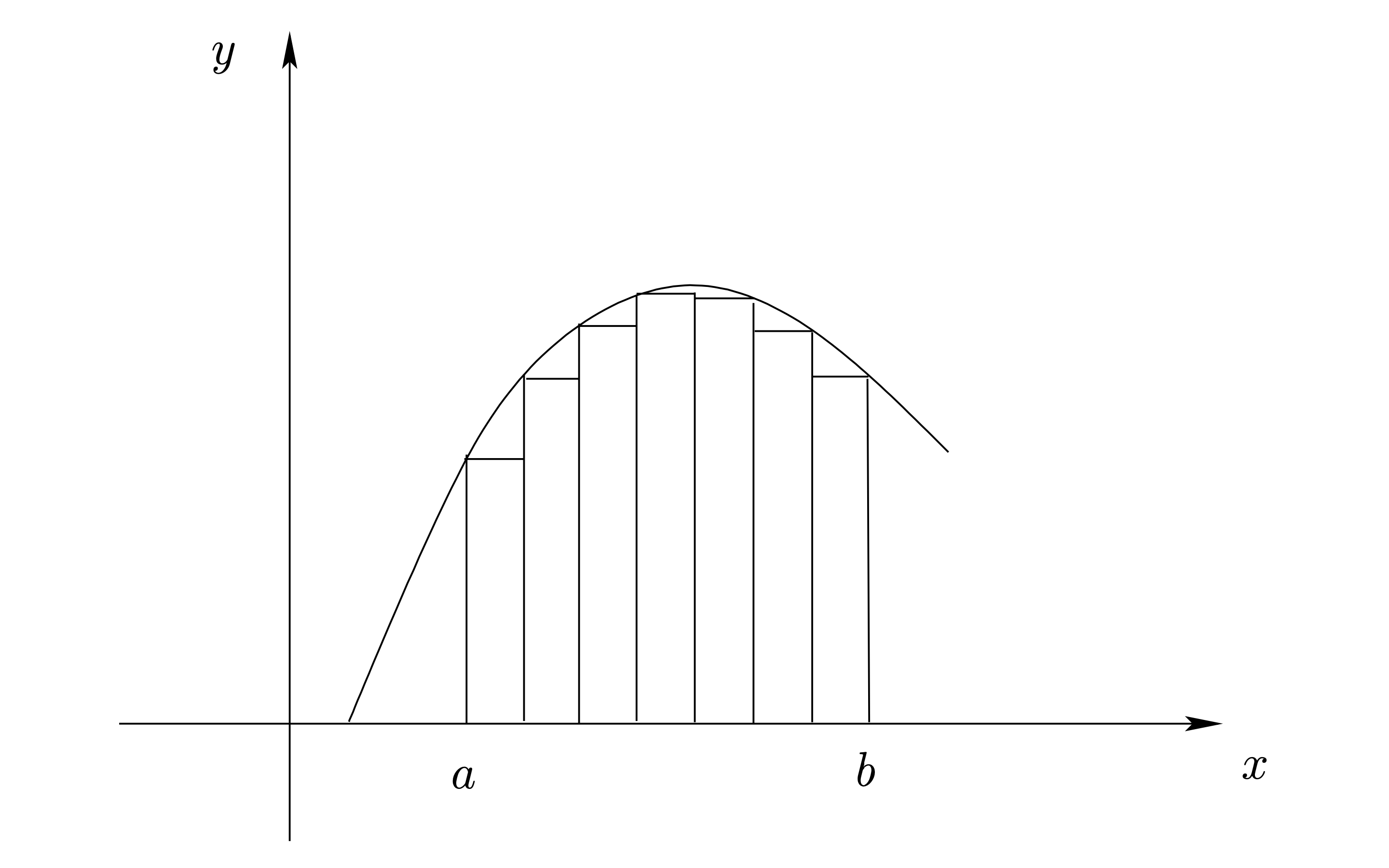
Figure 2.2: การหาพื้นที่ใต้กราฟ

ขั้นตอนเบื้องต้นสำหรับการหาพื้นที่ใต้กราฟ

แบ่ง $[a,b]$ เป็นช่วงเล็กๆ
หาพื้นที่รวมของสี่เหลี่ยมผืนผ้าทั้งหมด
ทำซ้ำๆ โดยแบ่งช่วงให้เล็กมากขึ้น
พื้นที่ที่ได้จะ “เข้าใกล้” พื้นที่ที่ต้องการมากขึ้นทุกที

ตัวอย่าง 2.1 จงหาสมการของเส้นสัมผัสกราฟ $y=-x^{2}+6x-2$ ณ จุด $P_{0}(2,6)$

วิธีทำ เลือกจุด $P(x,y)$ โดยที่ $x \neq 2$ และลากเส้น $PP_{0}$ จะได้ว่า ความชันของ $PP_{0}$ เท่ากับ

\[\begin{equation} \begin{aligned} \frac{y-6}{x-2} &= \frac{-x^{2}+6x-8}{x-2} \\ &=-\frac{\left( x-2\right) \left( x-4\right) }{x-2} \\ &=4-x \end{aligned} \end{equation}\]

ถ้า $P$ อยู่ใกล้ $P_{0}$ มากขึ้น ค่า x ย่อมเกือบเป็น 2 ดังนั้น ความชันของ $PP_{0}$ จึงเข้าใกล้ $4-2 = 2$ มากขึ้นเรื่อย ๆ เส้นสัมผัสจึงควรมีความชันเป็น 2 และสมการเส้นสัมผัส คือ $y-6=2\left( x-2\right)$

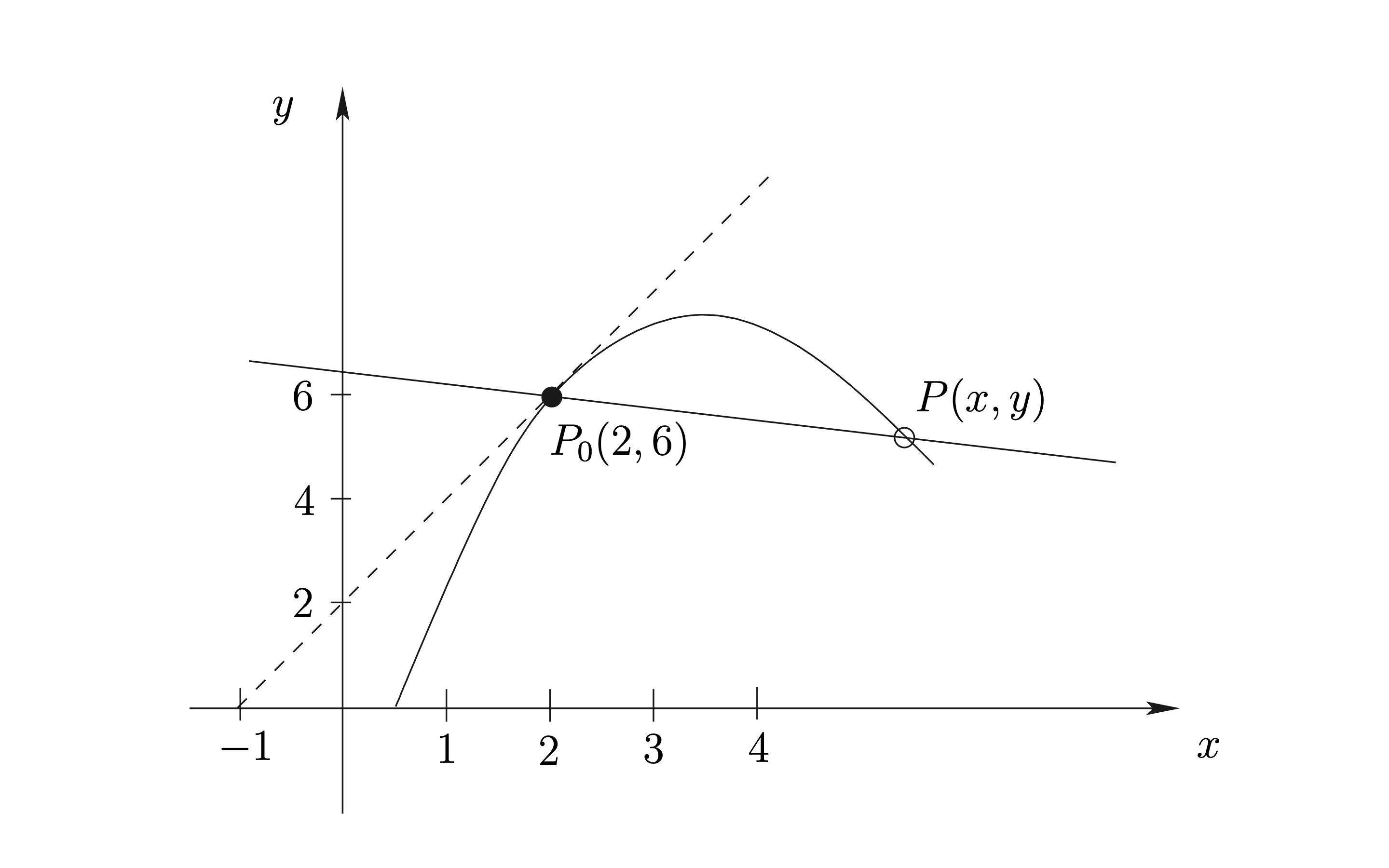
$การหาเส้นตรงที่สัมผัสเส้นโค้ง $y=-x^{2}+6x-2$$

Figure 2.3: การหาเส้นตรงที่สัมผัสเส้นโค้ง $y=-x^{2}+6x-2$

จะเห็นว่า ในตัวอย่าง 2.1 นี้ เราสนใจพฤติกรรมของ function

$\frac{-x^{2}+6x-8}{x-2}$ เมื่อ $x \neq 2$ แต่มีค่าใกล้ 2 มาก ๆ นี่คือ ที่มาของเรื่อง

นิยาม 2.1 ให้ $f : D_{f}\rightarrow R$ โดยที่ $D_{f}\subseteq R$ และให้ $a \in R$ โดยที่มีช่วง $(a,b)$ บางช่วงที่ $\left( a,b\right) \subseteq D_{f}\left( b>a\right)$

เรากล่าวว่า “ลิมิต (limit) ของ $f(x)$ เมื่อ x เข้าใกล้ a ทางขวา หาค่าได้และมีค่าเท่ากับจำนวนจริง L” ถ้า “ไม่ว่าเราจะกำหนดบริเวณรอบ ๆ $L$ ไว้แคบเพียงใด เมื่อเราพิจารณาค่าของ $f(x)$ สำหรับค่า $x$ ที่มากกว่า a โดยที่ให้ค่า ของ $x$ ลดลงเรื่อย ๆ จนถีงจุดหนึ่ง ค่าของ $f(x)$ จะอยู่ในบริเวณรอบ ๆ $L$ ที่เรากำหนดไว้นั้น และยังคงเป็นเช่นนี้สำหรับ $x$ อื่น ๆ ที่น้อยกว่านั้น (แต่มากกว่า $a$ ) ทั้งหมดด้วย”

ในทำนองเดียวกัน ถ้าเราพิจารณาพฤติกรรมของ function สำหรับ $x$ ที่น้อยกว่า $a$ จะได้ limit ทางซ้าย ดังนี้ ให้ $f : D_{f}\rightarrow R$ โดยที่ $D_{f}\subseteq R$ และให้ $a \in R$ โดยที่มีช่วง $(b,a)$ บางช่วงที่ $\left( b,a\right) \subseteq D_{f}\left( b<a\right)$

เรากล่าวว่า “limit ของ $f(x)$ เมื่อ $x$ เข้าใกล้ a ทางซ้าย หาค่าได้ และมีค่าเท่ากับจำนวนจริง $L$” ถ้า “ไม่ว่าเราจะกำหนดบริเวณรอบ ๆ $L$ ไว้แคบเพียงใด

เมื่อเราพิจารณาค่าของ $f(x)$ สำหรับค่า $x$ ที่น้อยกว่า $a$ โดยที่ให้ค่า ของ $x$ เพิ่มขึ้นเรื่อย ๆ จนถีงจุดหนึ่ง ค่าของ $f(x)$ จะอยู่ในบริเวณรอบ ๆ $L$ ที่เรากำหนดไว้นั้น และยังคงเป็นเช่นนี้สำหรับ $x$ อื่น ๆ ที่มากกว่านั้น (แต่น้อยกว่า $a$ ) ทั้งหมดด้วย”

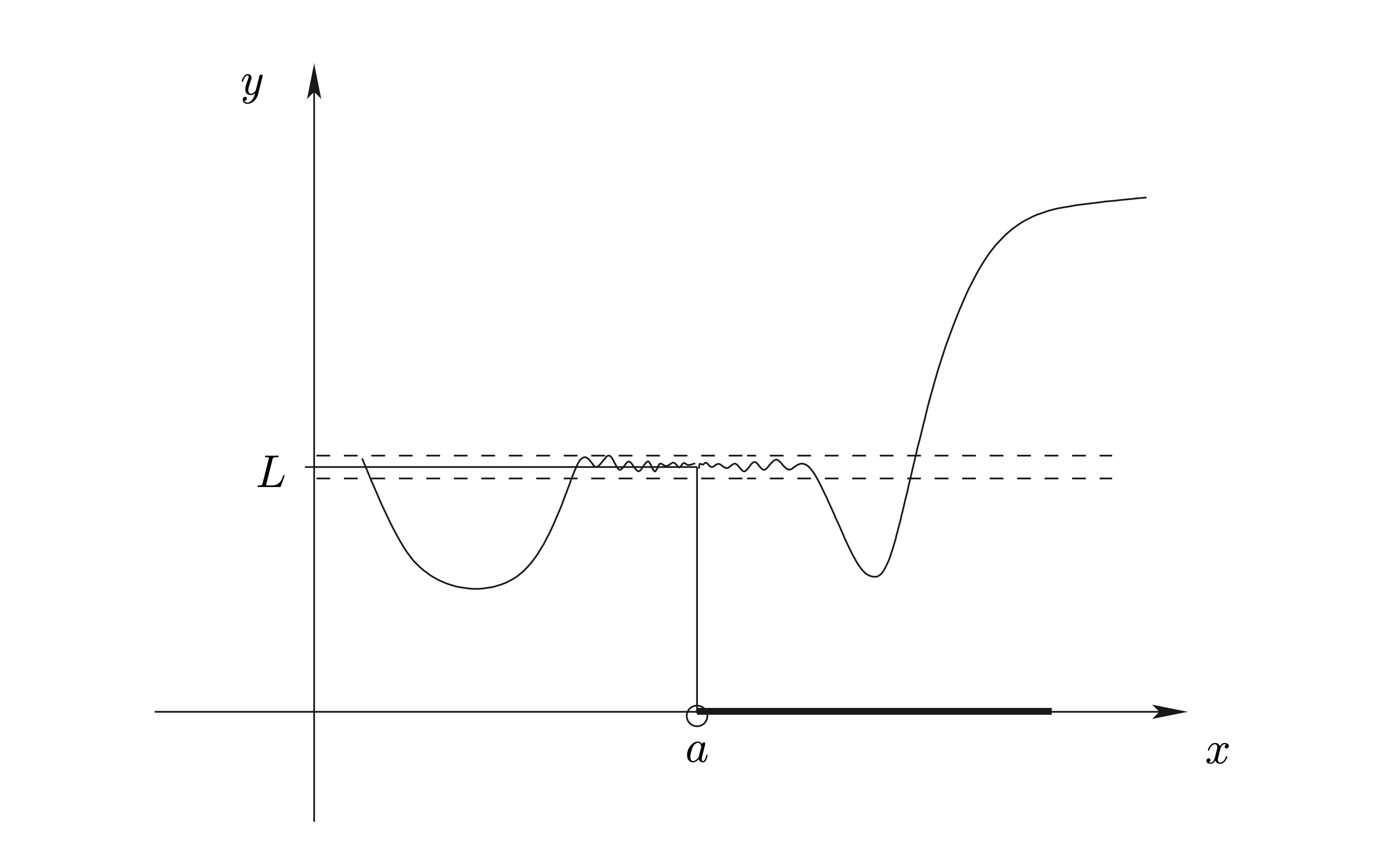
Figure 2.4: ลิมิตทางขวา

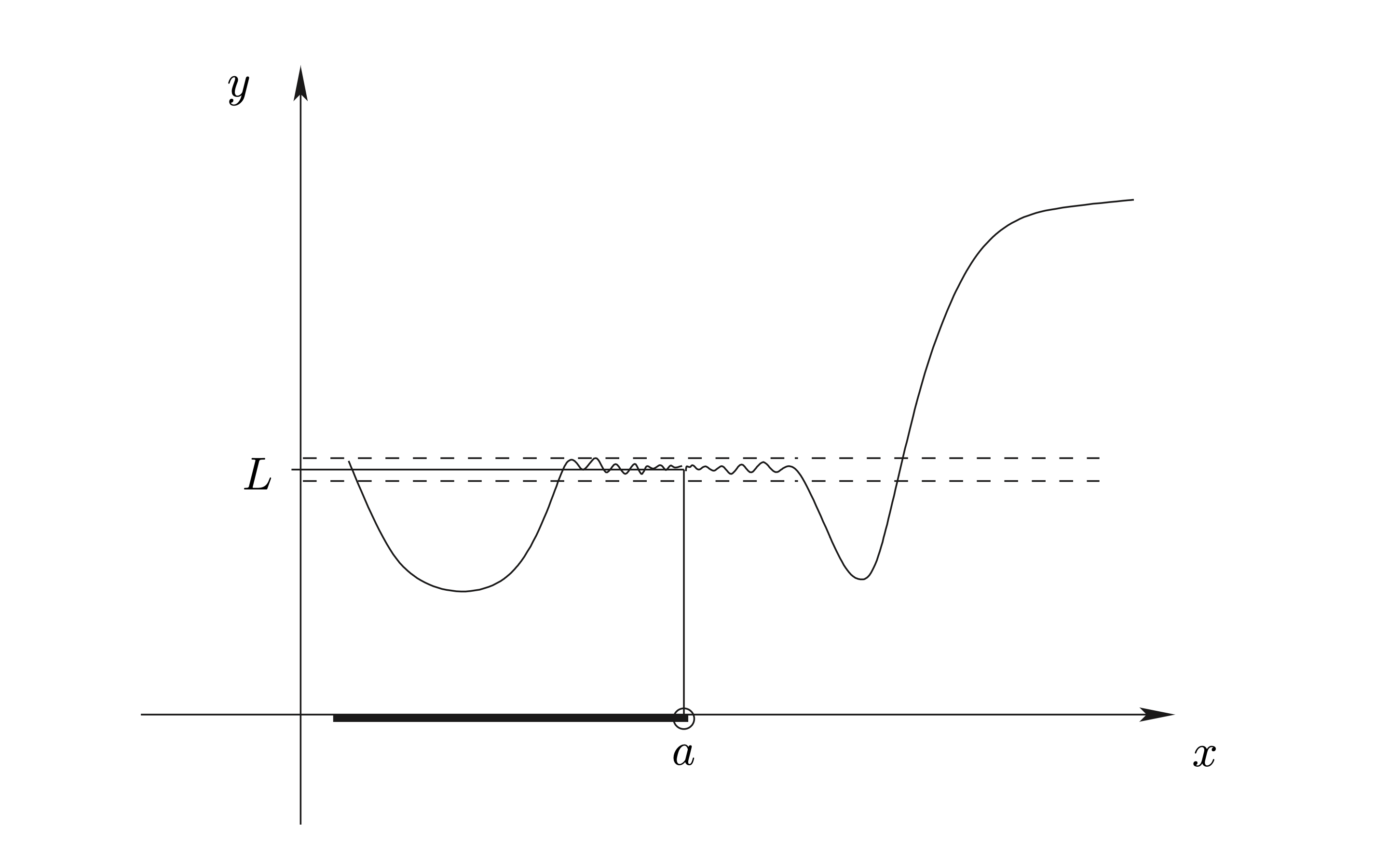
Figure 2.5: ลิมิตทางซ้าย

เราใช้สัญลักษณ์ $\underset{x\rightarrow a^{+}}{\lim}f(x)$ แทนข้อความ “limit ของ $f(x)$ เมื่อ $x$ เข้าใกล้ a ทางขวา” และใช้สัญลักษณ์ $\underset{x\rightarrow a^{-}}{\lim}f(x)$ แทนข้อความ “limit ของ $f(x)$ เมื่อ $x$ เข้าใกล้ a ทางซ้าย

นิยาม 2.2 ในกรณีที่ทั้ง $\underset{x\rightarrow a^{+}}{\lim}f(x)$ และ $\underset{x\rightarrow a^{-}}{\lim}f(x)$ หาค่าได้ และมีค่าเท่ากัน

เรากล่าวว่า $\underset{x\rightarrow a}{\lim}f(x)$ หาค่าได้ และมีค่าเท่ากับค่านั้น

ตัวอย่าง 2.2 function $f$ ที่ $\underset{x\rightarrow a^{+}}{\lim}f(x)$ หาค่าไม่ได้ ดังนั้น

$\underset{x\rightarrow a}{\lim}f(x)$ จึงหาค่าไม่ได้ด้วย

วิธีทำ จากรูปต่อไปนี้

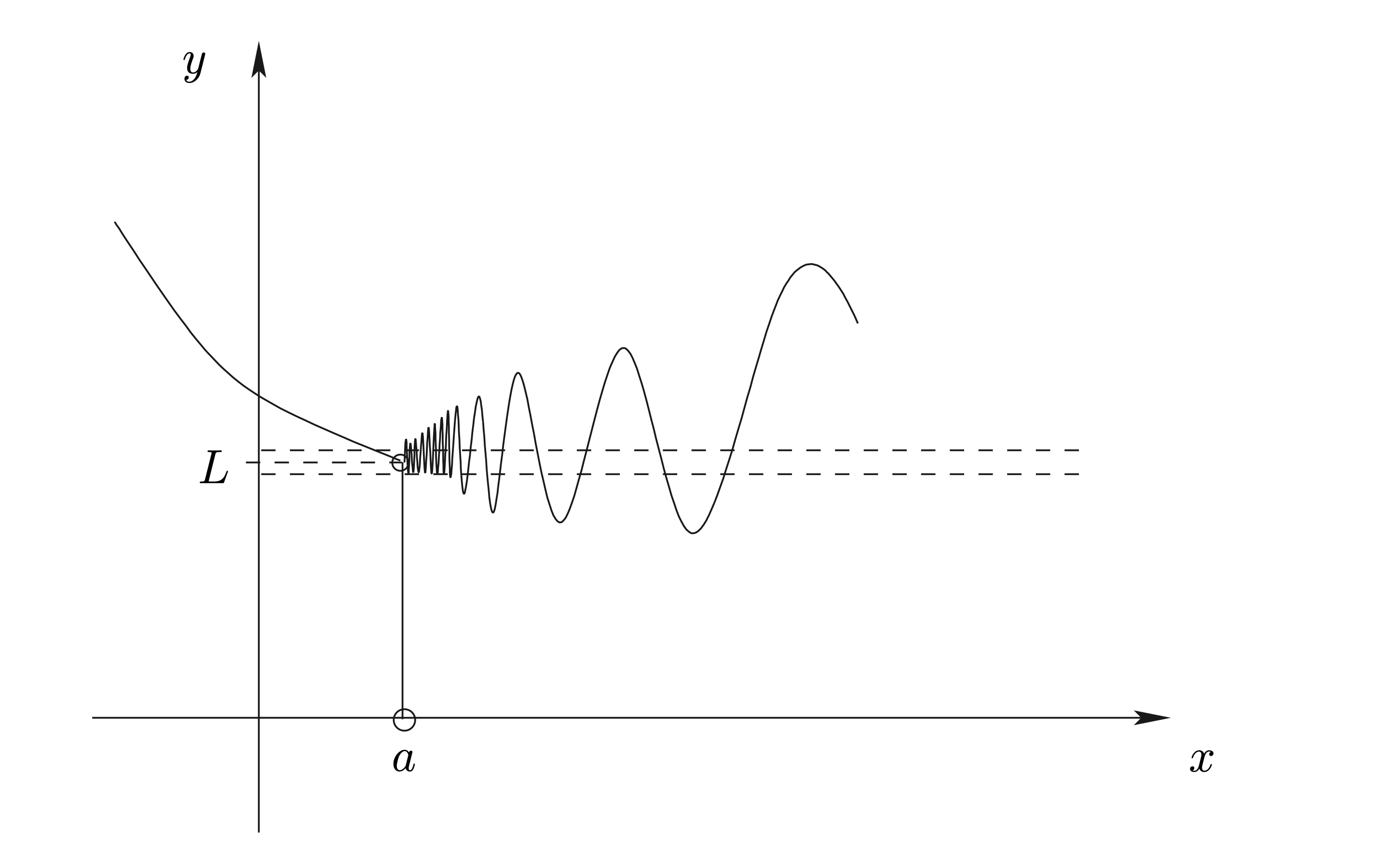
Figure 2.6: กราฟของฟังก์ชันที่หาลิมิตไม่ได้

ในกรณีนี้ จะเห็นว่า ไม่ว่าจะเลือก $L$ เป็นค่าใด ก็ไม่สามารถสรุปได้ว่า $\underset{x\rightarrow 0^{+}}{\lim}f(x)=L$ เพราะไม่ใช่ทุกครั้งที่เรากำหนดบริเวณรอบ ๆ $L$ แล้ว function จะสอดคล้องตามนิยามเสมอไป จึงสรุปว่า $\underset{x\rightarrow a}{\lim}f(x)=L$ หาค่าไม่ได้ด้วย

ทฤษฎี 2.1

$\underset{x\rightarrow c}{\lim}c=c$ ถ้า c เป็นจำนวนจริง
$\underset{x\rightarrow a}{\lim}x=a$

ทฤษฎี 2.2 ถ้า $\underset{x\rightarrow a}{\lim}f(x)$ และ $\underset{x\rightarrow a}{\lim}g(x)$ หาค่าได้แล้ว จะได้

$\underset{x\rightarrow a}{\lim}(f+g)(x)=\underset{x\rightarrow a}{\lim}f(x)+\underset{x\rightarrow a}{\lim}g(x)$
$\underset{x\rightarrow a}{\lim}(f-g)(x)=\underset{x\rightarrow a}{\lim}f(x)-\underset{x\rightarrow a}{\lim}g(x)$
$\underset{x\rightarrow a}{\lim}(f\cdot g)(x)=\left( \underset{x\rightarrow a}{\lim}f(x)\right) \cdot \left( \underset{x\rightarrow a}{\lim}g(x)\right)$
$\underset{x\rightarrow a}{\lim}\left( \frac{f}{g}\right) (x)=\frac{\underset{x\rightarrow a}{\lim}f(x)}{\underset{x\rightarrow a}{\lim}g(x)}$ ถ้า $\underset{x\rightarrow a}{\lim}g(x)\neq 0$

หมายเหตุ ทฤษฎีบททั้งสองนี้ยังคงเป็นจริงสำหรับ limit ทางซ้าย และ limit ทางขวาด้วย

ทฤษฎี 2.3 ถ้า $\underset{x\rightarrow a}{\lim}f(x)$ หาค่าได้ และ $\root{n}\of{f\left( x\right) }$ หาค่าได้ สำหรับทุก ๆ $x$ ในช่วงเปิดบางช่วงที่มี $a$ อยู่ด้วย แล้ว $\underset{x\rightarrow a}{\lim}\root{n}\of{f\left( x\right) }=\root{n}\of{\underset{x\rightarrow a}{\lim}f(x)}$

หมายเหตุ ทฤษฎีบทนี้เป็นจริงสำหรับ limit ทางซ้าย และ limit ทางขวาด้วย โดยเปลี่ยนเงื่อนไข “ทุก ๆ $x$” เป็น “ทุก ๆ $x < a$” และ “ทุก ๆ $x > a$” ตามลำดับ

ทฤษฎี 2.4 ถ้า $f$ และ $g$ เป็น function ซึ่ง $f\left( x\right) =g\left( x\right)$ สำหรับทุก ๆ $x$ ยกเว้นบาง $x$ ซึ่งมีอยู่เพียงจำนวนจำกัด แล้ว $\underset{x\rightarrow a}{\lim}f(x)=\underset{x\rightarrow a}{\lim}g(x)$ ถ้า limit อันใดอันหนึ่งหาค่าได้

หมายเหตุ ทฤษฎีบทนี้ยังคงเป็นจริงสำหรับ limit ทางซ้าย และ limit ทางขวาด้วย

ตัวอย่าง 2.3 จงหาค่าของ $\underset{x\rightarrow 2}{\lim}\frac{-x^{2}+6x-8}{x-2}$

วิธีทำ

\[\begin{equation} \begin{aligned} \lim_{x\rightarrow 2}\frac{-x^{2}+6x-8}{x-2} &= \lim_{x\rightarrow 2} -\frac{\left( x-2\right) \left( x-4\right) }{x-2}\\ &= \lim_{x\rightarrow 2} -\left( x-4\right) \\ %ต่างกับ function เดิม ที่ค่าเดียของ x คือ x = 2 &= \lim_{x\rightarrow 2}\left( 4-x\right) \\ &= \lim_{x\rightarrow 2}4-\lim_{x\rightarrow 2}x\\ &= 4-2 \\ &= 2 \end{aligned} \end{equation}\]

ตัวอย่าง 2.4 จงหาค่าของ $\underset{x\rightarrow 3}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$ วิธีทำ

\[\begin{equation} \begin{aligned} \lim_{x\rightarrow 3}\frac{\sqrt{x}-\sqrt{3}}{x-3} &= \lim_{x\rightarrow 3}\frac{\sqrt{x}-\sqrt{3}}{x-3}\cdot \frac{\sqrt{x}+\sqrt{3}}{\sqrt{x}+\sqrt{3}} \\ &= \lim_{x\rightarrow 3}\frac{x-3}{\left( x-3\right) \left( \sqrt{x}+\sqrt{3}\right) } \\ &= \lim_{x\rightarrow 3}\frac{1}{\sqrt{x}+\sqrt{3}}\\ &= \frac{\lim_{x\rightarrow 3}1}{\lim_{x\rightarrow 3} \sqrt{x} + \lim_{x\rightarrow 3} \sqrt{3}} \\ &= \frac{\lim_{x\rightarrow 3}1}{\sqrt{\lim_{x\rightarrow 3}x}+\lim_{x\rightarrow 3}\sqrt{3}} \\ &= \frac{1}{\sqrt{3}+\sqrt{3}} \\ &= \frac{1}{2\sqrt{3}} \\ \end{aligned} \end{equation}\]

ตัวอย่าง 2.5 จงหา limits ต่อไปนี้

$\underset{x\rightarrow 0^{+}}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$
$\underset{x\rightarrow 0^{-}}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$
$\underset{x\rightarrow 0}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$

วิธีทำ

$\underset{x\rightarrow 0^{+}}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$$=\frac{0-\sqrt{3}}{x-3}=\frac{\sqrt{3}}{3}$
เนื่องจาก function $\frac{\sqrt{x}-\sqrt{3}}{x-3}$ ไม่ใช่ function ที่หาค่าได้บนช่วงเปิด $\left( b,0\right)$ ใด ๆ เลย ดังนั้น $\underset{x\rightarrow 0^{-}}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$ จึงหาค่าไม่ได้
เนื่องจาก $\underset{x\rightarrow 0^{-}}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$ หาค่าไม่ได้ ดังนั้น $\underset{x\rightarrow 0}{\lim}\frac{\sqrt{x}-\sqrt{3}}{x-3}$ จึงหาค่าไม่ได้

ข้อสังเกต ในกรณีที่ function ที่มีค่ามากขึ้นโดยไม่มีขอบเขต เมื่อตัวแปรต้นเข้าใกล้ $a$ (ทางซ้ายหรือขวา หรือทั้งสองทาง) บางตำรากล่าวว่า limit ของ function มีค่าเป็น $+\infty$ และถ้า function มีค่าลดลงโดยไม่มีขอบเขต จะกล่าวว่า limit ของ function มีค่าเป็น $-\infty$ ในวิชานี้เราจะถือตามนิยามที่ให้ไว้ ดังนั้นในกรณีข้างต้น จะกล่าวว่า limit ดังกล่าวหาค่าไม่ได้ (เว้นแต่จะระบุให้พิจารณาค่า $\pm \infty$ ด้วย)

ตัวอย่าง 2.6 จงหา limit ของ function $f\left( x\right) =\frac{1}{x}$

เมื่อ $x$ เข้าใกล้ 0 ทางซ้าย
เมื่อ $x$ เข้าใกล้ 0 ทางขวา
เมื่อ $x$ เข้าใกล้ 0

วิธีทำ

$\underset{x\rightarrow 0^{-}}{\lim}\frac{1}{x}$ หาค่าไม่ได้ (หรือเท่ากับ $-\infty$)
$\underset{x\rightarrow 0^{+}}{\lim}\frac{1}{x}$ หาค่าไม่ได้ (หรือเท่ากับ $+\infty$)
$\underset{x\rightarrow 0}{\lim}\frac{1}{x}$ หาค่าไม่ได้

ในบางครั้ง เราสนใจพฤติกรรมของ function $f$ เมื่อค่าตัวแปรต้นมีค่ามากขึ้นโดยไม่มีขอบเขต หรือน้อยลงโดยไม่มีขอบเขต ในกรณีเช่นนี้ เราใช้สัญลักษณ์ $\underset{x\rightarrow +\infty }{\lim}f\left( x\right)$ และ $\underset{x\rightarrow -\infty }{\lim}f\left( x\right)$ ตามลำดับ แทนที่จะใช้ $\underset{x\rightarrow \infty ^{-}}{\lim}f\left( x\right)$ และ $\underset{x\rightarrow \infty ^{+}}{\lim}f\left( x\right)$ (โปรดอ่านนิยามในเอกสารอ้างอิง) ทฤษฎีบทเกี่ยวกับ limit ที่กล่าวมาข้างต้นทั้งหมด เป็นจริงในกรณีนี้ด้ย นอกจากนี้ เรายังมี ทฤษฎีบทต่อไปนี้

ทฤษฎี 2.5

$\underset{x\rightarrow +\infty }{\lim}x=+\infty$
$\underset{x\rightarrow -\infty }{\lim}x=-\infty$
ถ้า $\underset{x\rightarrow a}{\lim}f\left( x\right) =\pm \infty$ แล้ว $\underset{x\rightarrow a}{\lim}f\left( x\right) =0$ ซึ่งเป็นจริงสำหรับ limit ทางซ้าย และ limit ทางขวาด้วย ในที่นี้ $a\in R$ หรือ a เป็น $+\infty$ หรือ $-\infty$

ตัวอย่าง 2.7 $\underset{x\rightarrow -\infty }{\lim}\frac{x^{2}+12}{x^{3}-5}=?$

วิธีทำ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow -\infty }{\lim}\frac{x^{2}+12}{x^{3}-5} &=\underset{x\rightarrow -\infty }{\lim}\frac{\left( x^{2}+12\right) /x^{3}}{\left( x^{3}-5\right) /x^{3}} \\ &=\underset{x\rightarrow -\infty }{\lim}\frac{\frac{1}{x}+\frac{12}{x^{3}}}{1-\frac{5}{x^{3}}} =\frac{0+0}{1-0}=0 \end{aligned} \end{equation}\]

ตัวอย่าง 2.8 $\underset{x\rightarrow +\infty }{\lim}x^{-\frac{2}{3}}=?$

วิธีทำ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow +\infty }{\lim}x^{-\frac{2}{3}} &=\underset{x\rightarrow +\infty }{\lim}\root{3}\of{\left( \frac{1}{x}\right) ^{2}} \\ &=\root{3}\of{\left( \underset{x\rightarrow +\infty }{\lim}\frac{1}{x}\right) ^{2}} =0 \end{aligned} \end{equation}\]

ตัวอย่าง 2.9 $\underset{x\rightarrow +\infty }{\lim}\frac{x^{\frac{1}{3}}+3x^{\frac{1}{5}}+5x^{\frac{1}{7}}}{3x^{\frac{1}{3}}+5x^{\frac{1}{5}}+7x^{\frac{1}{7}}}=?$

วิธีทำ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow +\infty }{\lim}\frac{x^{\frac{1}{3}}+3x^{\frac{1}{5}}+5x^{\frac{1}{7}}}{3x^{\frac{1}{3}}+5x^{\frac{1}{5}}+7x^{\frac{1}{7}}} &=\underset{x\rightarrow +\infty }{\lim}\frac{x^{\frac{1}{3}}\left( 1+3x^{-\frac{2}{15}}+5x^{-\frac{4}{21}}\right) }{x^{\frac{1}{3}}\left( 3+5x^{-\frac{2}{15}}+7x^{-\frac{4}{21}}\right) } \\ &=\underset{x\rightarrow +\infty }{\lim}\frac{1+3x^{-\frac{2}{15}}+5x^{-\frac{4}{21}}}{3+5x^{-\frac{2}{15}}+7x^{-\frac{4}{21}}} =\frac{1}{3} \end{aligned} \end{equation}\]

ข้อสังเกต ตัวแปร $x$ ในสัญลักษณ์ $\underset{x\rightarrow a}{\lim}f\left( x\right)$ เรียกว่า “ตัวแปรหุ่น” (dummy variable) เพราะไม่ได้กล่าวถึงตัวแปร $x$ แต่เราใช้มันเพื่อเขียนสัญลักษณ์แทนจำนวนจริงจำนวนหนึ่งที่ค่าของ function $f$ ใกล้เข้าไปหา ในยามที่ตัวแปรต้นของมันมีค่าใกล้ $a$ เข้าไปทุกที เราอาจเขียน $\underset{t\rightarrow a}{\lim}f\left( t\right)$ แทนจำนวนจำนวนนี้ก็ได้ เป็นต้น ตัวอย่างของ dummy variable อื่น ๆ เช่น ตัวแปร $n$ ในสัญลักษณ์ $\underset{n=1}{\overset{4}{\sum }}n^{2}$ ซึ่งอาจเขียนใหม่เป็น $\underset{k=1}{\overset{4}{\sum }}k^{2}$ ก็ได้ ทั้งสองสัญลักษณ์นี้แทนจำนวน $1^{2}+2^{2}+3^{3}+4^{4}$

ตัวอย่าง 2.10 จงหา $\underset{x\rightarrow 3}{\lim}f\left( x\right)$ เมื่อ

\[ f(x) = \begin{cases} x^2 - 5 & \text{ถ้า } x \leq 3 \\ \sqrt{x + 13} & \text{ถ้า } x > 3 \end{cases} \]

วิธีทำ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow 3^{-}}{\lim}f\left( x\right) &=\underset{x\rightarrow 3^{-}}{\lim}x^{2}-5 \leftarrow \boxed{ f(x) = x^{2}-5 \mbox{ เมื่อ $x$ อยู่ทางซ้ายของ 3}}\\ &=4 \end{aligned} \end{equation}\] \[\begin{equation} \begin{aligned} \underset{x\rightarrow 3^{+}}{\lim}f\left( x\right) &= \underset{x\rightarrow 3^{+}}{\lim}\sqrt{x+13} \leftarrow \boxed{ f(x)=\sqrt{x+13} \mbox{ เมื่อ $x$ อยู่ทางขวาของ 3}} \\ &=4 \end{aligned} \end{equation}\]

เนื่องจาก $\underset{x\rightarrow 3^{-}}{\lim}f\left( x\right) =$ $\underset{x\rightarrow 3^{+}}{\lim}f\left( x\right) =4$ ดังนั้น $\underset{x\rightarrow 3}{\lim}f\left( x\right)$ หาค่าได้ และมีค่าเท่ากับ 4

ตัวอย่าง 2.11 จงหา $\underset{x\rightarrow 0}{\lim}f\left( x\right)$ เมื่อ \[f(x) = \begin{cases} x^{2}-5 & \text{ ถ้า } x\leq 3 \\ \sqrt{x+13} & \text{ ถ้า } x>3 \end{cases}\]

วิธีทำ $\underset{x\rightarrow 0}{\lim}f(x)=\underset{x\rightarrow 0}{\lim}(x^{2}-5)=-5$

2.1 ความต่อเนื่อง (Continuity)

ในวิชาฟิสิกส์ เราสามารถเขียนตำแหน่งของวัตถุที่กำลังเคลื่อนที่ในรูป function ของเวลาได้ (วัตถุย่อมอยู่ในที่ใดที่หนึ่งเพียงที่เดียว ณ เวลาหนึ่ง ๆ)

คำถาม : function ใด ๆ เป็น function ที่แสดงตำแหน่งของวัตถุใดวัตถุหนึ่งได้เสมอหรือไม่

ลองอธิบายการเคลื่อนที่ของวัตถุ ถ้า function ที่แสดงตำแหน่งของมัน คือ

$s_{1}(t) = \begin{cases} 1 & \text{ ถ้า } t<3 \\ 1 & \text{ ถ้า } t>3 \end{cases}$
$s_{2}(t) = \begin{cases} 0 & \text{ ถ้า } t \le 3 \\ 1 & \text{ ถ้า } t>3 \end{cases}$
$s_{3}(t) = \begin{cases} 1 & \text{ ถ้า } t \neq 3 \\ 0 & \text{ ถ้า } t=3 \end{cases}$

กราฟของ $s_1,s_2$ และ $s_3$ เป็นดังนี้

ข้อสังเกต:

$s_1(3)$ หาค่าไม่ได้
$s_2(3)$ หาค่าได้ แต่ $\underset{t \rightarrow 3}{\lim} s_2(t)$ หาค่าไม่ได้
$s_3(3)$ หาค่าได้ $\underset{t \rightarrow 3}{\lim} s_3(t)$ หาค่าได้ แต่ $s_3(3) \neq \underset{t \rightarrow 3}{\lim} s_3(t)$

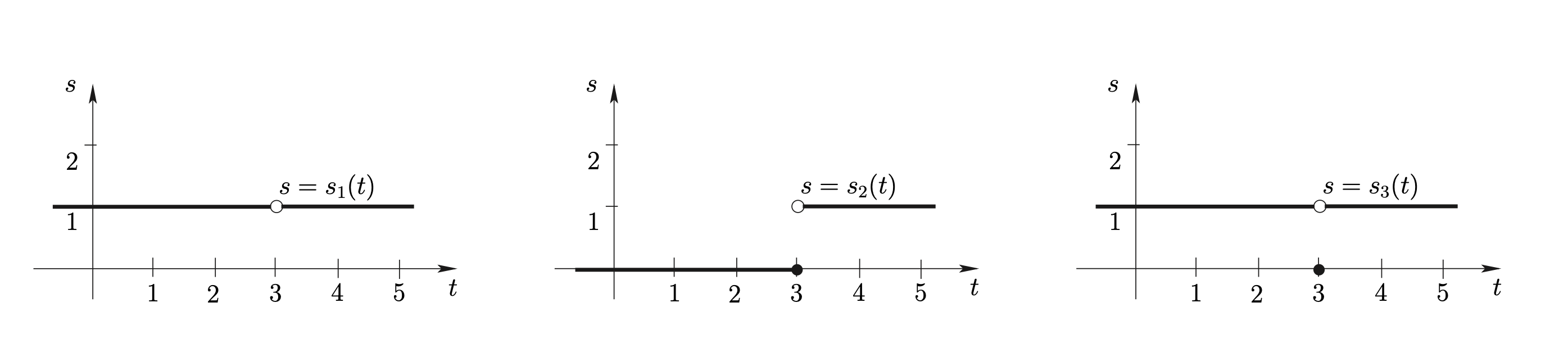
Figure 2.7: กราฟของฟังก์ชัน $s_1$, $s_2$ และ $s_3$

นิยาม 2.3 ให้ $f:D_{f}\rightarrow R$ โดยที่ $D_{f}\subseteq R$ และ $a\in R$ เรากล่าวว่า $f$ ต่อเนื่อง (cotinuous) ที่ $a$ ถ้า

$f \left( a\right)$ หาค่าได้
$\underset{x\rightarrow a}{\lim}f(x)$ หาค่าได้
$f\left( a\right) =\underset{x\rightarrow a}{\lim}f(x)$

นิยาม 2.4 ให้ $f$ เป็น function และ $S$ เป็นเซต (set) เรากล่าวว่า $f$ ต่อเนื่องบน $S$ (continuous on $S$) ถ้า $f$ ต่อเนื่องที่ทุก ๆ สมาชิกของ $S$ เรียก function ที่ continuous on $R$ ว่า “ฟังก์ชันต่อเนื่อง (continuous function)”

ข้อสังเกต จะเห็นว่า function ที่แสดงตำแหน่งของวัตถุต้องเป็น continuous function บนช่วงที่สนใจ

ทฤษฎี 2.6 ถ้า $f$ และ $g$ เป็น function ที่ต่อเนื่องที่ $a$ แล้ว

$f+g$ ต่อเนื่องที่ $a$
$f-g$ ต่อเนื่องที่ $a$
$f\cdot g$ ต่อเนื่องที่ $a$
$\frac{f}{g}$ ต่อเนื่องที่ $a$ ถ้า $g\left( a\right) \neq 0$

ตัวอย่าง 2.12 function $f$ ซึ่งนิยามโดย $f\left( x\right) =\left| x\right|$ เป็นฟังก์ชันต่อเนื่องหรือไม่

วิธีทำ ในที่นี้ \[f\left( x\right) = \begin{cases} x & \text{ ถ้า } x \ge 0 \\ -x & \text{ ถ้า } x>0 \end{cases}\] เราต้องพิจารณาว่า $f$ ต่อเนื่องที่ทุก ๆ $a\in R$ หรือไม่

ถ้า $a>0$ จะได้ $\underset{x\rightarrow a}{\lim}f(x)=\underset{x\rightarrow a}{\lim}x=a=f(a)$
ถ้า $a<0$ จะได้ $\underset{x\rightarrow a}{\lim}f(x)=\underset{x\rightarrow a}{\lim}(-x)=-a=f(a)$
ถ้า $a=0$จะได้ $\underset{x\rightarrow 0^{-}}{\lim}f(x)=\underset{x\rightarrow 0^{-}}{\lim}(-x)=0=f(0)$
และ $\underset{x\rightarrow 0^{+}}{\lim}f(x)=\underset{x\rightarrow 0^{+}}{\lim}x=0=f(0)$
ดังนั้น $\underset{x\rightarrow 0}{\lim}f(x)=0=f(0)$

ดังนั้น $f$ ต่อเนื่องที่ทุก ๆ $a\in R$ จึงสรุปว่า $f$ เป็น continuous function

ทฤษฎี 2.7 ฟังก์ชันตรรกยะ (rational function) เป็น function ที่ต่อเนื่องบน domain ของมัน

หมายเหตุ: rational function คือ function ที่เป็นเศษส่วนของพหุนาม (polynomial) domain ของ rational function ได้แก่เซตของจำนวนจริงซึ่งไม่ทำให้ส่วนของมันเป็นศูนย์

ทฤษฎี 2.8 ถ้า $f$ และ $g$ เป็น function และ $a\in R$ โดยที่ $\underset{x\rightarrow a}{\lim}g(x)=L$ และ $f$ ต่อเนื่องที่ $L$ แล้ว $\underset{x\rightarrow a}{\lim}f(g(x))=f(\underset{x\rightarrow a}{\lim}g(x))=f(L)$

ตัวอย่าง 2.13 $\underset{x\rightarrow 1}{\lim}\left| \frac{x^{4}-x^{2}+1}{x^{4}+x^{2}+1}\right| =?$

วิธีทำ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow 1}{\lim}\left| \frac{x^{4}-x^{2}+1}{x^{4}+x^{2}+1}\right| &=\left| \ \underset{x\rightarrow 1}{\lim}\frac{x^{4}-x^{2}+1}{x^{4}+x^{2}+1}\right| \\ &=\left| \frac{1^{4}-1^{2}+1}{1^{4}+1^{2}+1}\right| \\ &=\left| \frac{1}{3}\right| =\frac{1}{3} \end{aligned} \end{equation}\]

ทฤษฎี 2.9 ถ้า $f$ ต่อเนื่องที่ $a$ และ $g$ ต่อเนื่องที่ $f(a)$ แล้ว $g\circ f$ ต่อเนื่องที่ $a$

จงพิสูจน์ทฤษฎีบทข้างต้น

ตัวอย่าง 2.14 function f ซึ่งนิยามโดย $\ f\left( x\right) =\left| \frac{x^{4}-x^{2}+1}{x^{4}+x^{2}+1}\right|$ เป็น continuous function หรือไม่

วิธีทำ $f$ เป็น continuous function เพราะ $f =g\circ h$ โดยที่ $g\left( x\right) =\left| x\right|$ และ $h\left( x\right) =\frac{x^{4}-x^{2}+1}{x^{4}+x^{2}+1}$ ซึ่งเป็น continuous function ทั้งคู่

นิยาม 2.5 เรานิยาม “ภาวะต่อเนื่องทางซ้าย” และ “ภาวะต่อเนื่องทางขวา” ได้โดยแทนที่ $\underset{x\rightarrow a}{\lim}$ ในเงื่อนไขของนิยาม ด้วย $\underset{x\rightarrow a^{-}}{\lim}$ และ $\underset{x\rightarrow a^{+}}{\lim}$ ตามลำดับ นั่นคือ

ให้ $f:D_{f}\rightarrow R$ โดยที่ $D_{f}\subseteq R$ และ $a\in R$ เรากล่าวว่า $f$ “ต่อเนื่องทางซ้าย (left-continuous) ที่ $a$” ถ้า

$f\left( a\right)$ หาค่าได้
$\underset{x\rightarrow a^{-}}{\lim}f(x)$ หาค่าได้
$f\left( a\right) =\underset{x\rightarrow a^{-}}{\lim}f(x)$

และกล่าวว่า $f$ “ต่อเนื่องทางขวา (right-continuous) ที่ $a$” ถ้า

f$\left( a\right)$ หาค่าได้
$\underset{x\rightarrow a^{+}}{\lim}f(x)$ หาค่าได้
f$\left( a\right) =\underset{x\rightarrow a^{+}}{\lim}f(x)$

นิยาม 2.6 ให้ $f : \left[ a,b\right] \rightarrow R$ เรากล่าวว่า $f$ ต่อเนื่องบน $\left[ a,b\right]$ (continuous on $\left[ a,b\right]$) ถ้า

$f$ ต่อเนื่องบน $(a,b)$
$f$ ต่อเนื่องทางขวาที่ $a$
$f$ ต่อเนื่องทางซ้ายที่ $b$

ตัวอย่าง 2.15 function $f$ ที่นิยามโดย $f\left( x\right) =\sqrt{4-x^{2}}$ เป็น continuous function บน $\left[ -2,2\right]$ หรือไม่

วิธีทำ เราตรวจสอบได้ว่า $f$ เป็น continuous function บน $\left[ -2,2\right]$ เพราะ
1. $f$ เป็น continuous function บน $\left( -2,2\right)$
2. $f$ ต่อเนื่องทางขวาที่ -2 เพราะ $$

\[\begin{equation} \begin{aligned} \underset{x\rightarrow -2^{+}}{\lim}f(x) &=\underset{x\rightarrow -2^{+}}{\lim}\sqrt{4-x^{2}} \\ &=0=f\left( -2\right) \end{aligned} \end{equation}\]

$f$ ต่อเนื่องทางซ้าย ที่ 2 เพราะ

\[\begin{equation} \begin{aligned} \underset{x\rightarrow -2^{-}}{\lim}f(x) &=\underset{x\rightarrow -2^{-}}{\lim}\sqrt{4-x^{2}} \\ &=0 =f\left( 2\right) \end{aligned} \end{equation}\]

ตัวอย่าง 2.16 พิจารณา function f ซึ่งมีกราฟดังต่อไปนี้

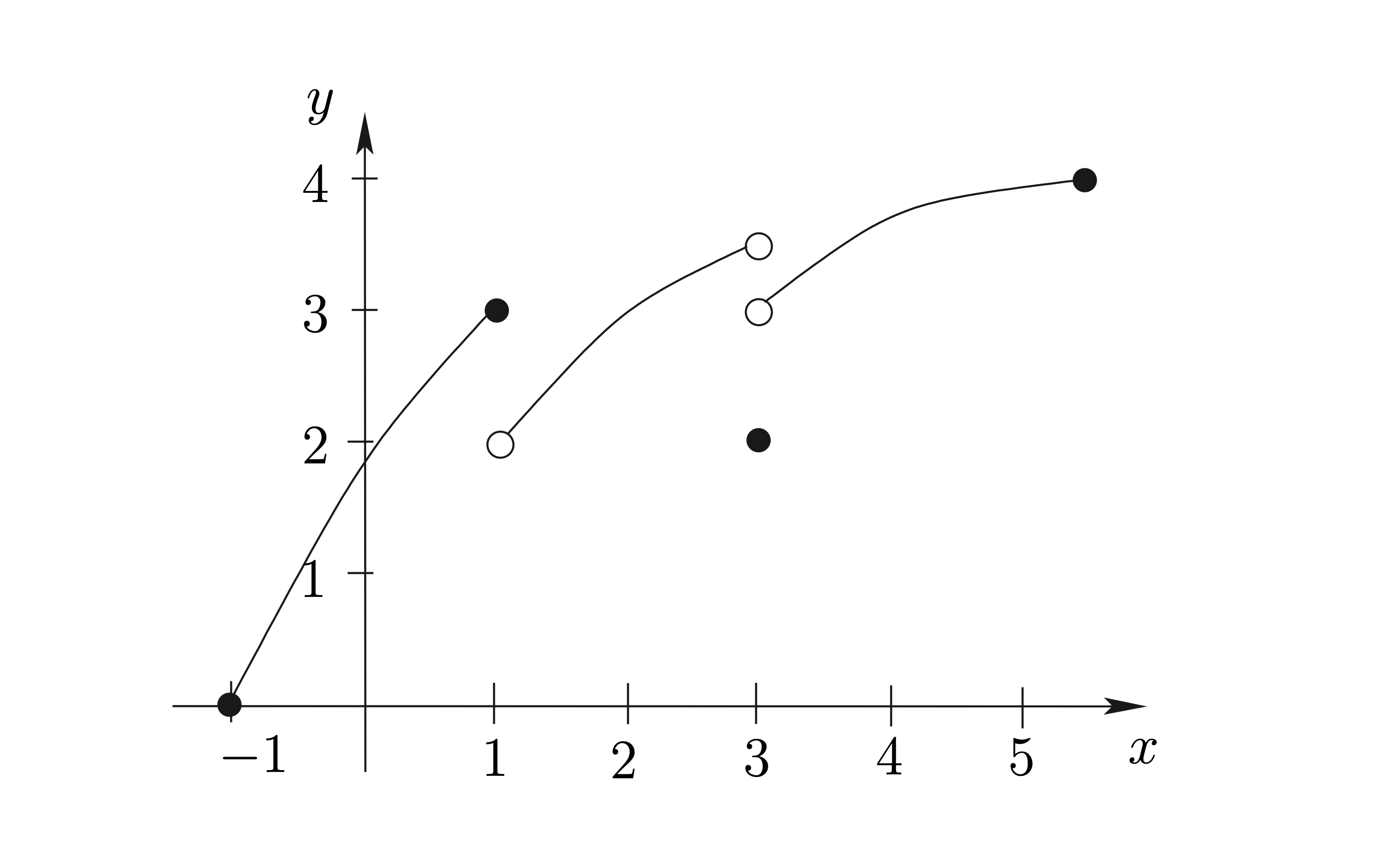
$กราฟของฟังก์ชันในตัวอย่าง \@ref(exm:ex-cont-5)$

Figure 2.8: กราฟของฟังก์ชันในตัวอย่าง 2.16

$f$ มีความต่อเนื่องที่ $-1,0,1,2,3,4,5$ หรือไม่
$f$ มีความต่อเนื่องบน $\left[ -1,0\right] ,\left[ 0,1\right] ,\left[ 1,2\right] ,\left[ 2,3\right] ,\left[ 3,4\right] ,\left[ 4,5\right]$ หรือไม่

วิธีทำ ให้นักศึกษาทำเป็นแบบฝึกหัด

ทฤษฎี 2.10 ฟังก์ชันตรีโกณมิติ ฟังก์ชันตรีโกณมิติผกผัน ฟังก์ชันเลขชี้กำลัง และฟังก์ชันลอการิทึม เป็นฟังก์ชันที่ต่อเนื่องบนโดเมนของมัน