บทที่ 5 การหาปริพันธ์ (Integrations)

5.1 ปฏิยานุพันธ์ (Antiderivatives)

จากเรื่องการหาอนุพันธ์ ถ้าวัตถุชนิดหนึ่งมีสมการการเคลื่อนที่ คือ \(s = t^{3}\) โดยที่วัตถุนี้เคลื่อนที่ได้ระยะทาง \(s\) เมตร เมื่อเวลาผ่านไป \(t\) วินาที แล้วเราสามารถบอกได้ว่าวัตถุเคลื่อนที่ด้วยความเร็ว \(v = 3t^2\) เมตร/วินาที แต่เรารู้ว่า \(\displaystyle v = \frac{ds}{dt}\) ดังนั้น \(\displaystyle \frac{ds}{dt} = 3t\) ในทางกลับกันถ้าเรารู้ว่าสมการความเร็วของวัตถุชนิดหนึ่ง ถ้า \(v = 3t^{2}\) แสดงว่า \(\displaystyle \frac{ds}{dt} = 3t^2\) แล้วลองนึกย้อนกลับว่าสมการการเคลื่อนที่ของวัตถุชนิดนี้ คือ สมการใด จะเห็นว่าสมการการเคลื่อนที่ของวัตถุนี้อาจจะอยู่ในรูป

\[\begin{equation} \begin{aligned} s &= t^3 \\ s &= t^3 -2 \\ \text{หรือ } s &= t^3 + 5 \end{aligned} \end{equation}\]

ซึ่งทั้งสามสมการนี้มี \(\displaystyle \frac{ds}{dt}= 3t^2\) แต่เราก็ยังไม่แน่ใจว่าเป็นสมการใดกันแน่หรืออาจไม่ใช่ทั้งสามสมการนี้ก็ได้ แต่เราสามารถคาดคะเนได้ว่าสมการการเคลื่อนที่ของวัตถุนี้ควรจะอยู่ในรูป \[s = t^{3} + c\] โดยที่ \(c\) เป็นค่าคงตัว สมการการเคลื่อนที่ทั้งสี่สมการดังกล่าวนี้เป็นตัวอย่างของ “ปฏิยานุพันธ์” ของ \(v = 3t^{2}\)

ในกรณีทั่วไป เราจะนิยามปฏิยานุพันธ์ของฟังก์ชันดังต่อไปนี้

นิยาม 5.1 ฟังก์ชัน \(F\) เป็นปฏิยานุพันธ์ (antiderivative) ของฟังก์ชัน \(f\) บนช่วง \(I\) ถ้า \(F'(x) = f(x)\) สำหรับทุก ๆ ค่าของ \(x\) ในช่วง \(I\)

ตัวอย่าง 5.1 จงแสดงว่า \(F(x) = x^{2}-2x- 3\) เป็นปฏิยานุพันธ์ของฟังก์ชัน \(f(x)=2x-2\) บนช่วง \(\left( {-\infty ,\infty } \right)\)

วิธีทำ จาก \(F(x) = x^{2} - 2x - 3\) จะได้ \(F'(x) = 2x - 2\) นั่นคือ \(F'(x) = f(x)\) สำหรับทุก ๆ \(x\) ในช่วง \(\left( {-\infty ,\infty } \right)\)

ตัวอย่าง 5.2 ให้ \(f(x) = 2x^{3/2}\) จงหาปฏิยานุพันธ์ของ \(f\) บนช่วง \(\left( {0 ,\infty } \right)\)

วิธีทำ ให้ \(\displaystyle F_{1}(x) = \frac{4}{5} x^{5/2}\) จะได้ \(F'_1(x) = 2x^{3/2}\) สำหรับ \(x > 0\)

และให้ \(\displaystyle F_{2}(x) = \frac{4}{5} x^{5/2} + 2\) จะได้ \(F'_2(x) = 2x^{3/2}\) สำหรับ \(x > 0\)

และให้ \(\displaystyle F_{3}(x) = \frac{4}{5} x^{5/2} - 5\) จะได้ \(F'_3(x) = 2x^{3/2}\) สำหรับ \(x > 0\)

ดังนั้น \(F_1,F_2\) และ \(F_3\) ต่างก็เป็นปฏิยานุพันธ์ของ \(f(x) = 2x^{3/2}\) บนช่วง \(\left( {0 ,\infty } \right)\) และแต่ละค่าคงตัว \(C\) ถ้าให้ \(F(x) =(4/5)x^{5/2} + C\) จะทำให้ \(F'(x) = 2x^{3/2}\) สำหรับทุก \(x \in \left( 0 ,\infty \right)\)

ดังนั้น เราสามารถสรุปได้ว่าฟังก์ชัน \(F\) ใด ๆ ที่

\[\begin{equation} F(x) = \frac{4}{5} x^{5/2} + C \tag{5.1} \end{equation}\]

เป็นปฏิยานุพันธ์ของ \(f(x) = 2x^{3/2}\) บนช่วง \(\left( 0 ,\infty \right)\) เมื่อ \(C\) เป็นค่าคงตัว

จากตัวอย่างนี้ฟังก์ชัน \(F\) ที่นิยาม โดย (5.1) เป็นรูปทั่วไปของปฏิยานุพันธ์ของ \(f(x) = 2x^{3/2}\) บน \(\left( 0 ,\infty \right)\) และให้สังเกตว่าช่วง \(\left( 0 ,\infty \right)\) เป็นโดเมนของ \(f\)

ข้อสังเกต

ถ้า \(f\) และ \(g\) เป็นฟังก์ชันซึ่ง \(f^{'}(x) = g^{'}(x)\) สำหรับทุก ๆ \(x\) ในช่วง \(I\) แล้วจะมีค่าคงที่ \(K\) ที่ทำให้ \(f(x) = g(x) + K\)
ถ้า \(F\) เป็นปฏิยานุพันธ์เฉพาะของ \(f\) บนช่วง \(I\) แล้วแต่ละปฏิยานุพันธ์ของ \(f\) บนช่วง สามารถถูกเขียนได้ในรูป \(F(x) + C\) เมื่อ \(C\) เป็นค่าคงตัว

5.1.1 แบบฝึกหัด (Antiderivatives)

จงหาปฏิยานุพันธ์ของฟังก์ชันที่กำหนดให้ดังต่อไปนี้

\(f(x) = 0\)
\(f(x) = 4x\)
\(f(x) = 3x^{2 }\)
\(f(x) = x^{3}\)
\(f(x) = \sqrt{x}\)
\(f(x) = e^{x}\)
\(f(x) = \sin x\)
\(f(x) = \frac{1}{x^{2}+1}\)

เฉลยแบบฝึกหัด 5.1.1 กำหนดให้ \(C\) แทนค่าคงตัวใด ๆ

\(C\)
\(2x^{2} + C\)
\(x^{3} + C\)
\(\displaystyle \frac{x^{4}}{4}+c\)
\(\displaystyle \frac{2x^{3/2}}{3} + C\)
\(e^{x} + C\)
\(-\cos x + C\)
\(\tan^{-1}x + C\)

5.2 ปริพันธ์จำกัดเขต (The Definite Integral)

5.2.1 Integration คืออะไร

Integration Calculus เป็นวิชาที่เกี่ยวกับการคำนวณหา พื้นที่และปริมาตรของรูปทรงต่างๆโดยอาศัยหลัก การที่ว่า รูปทรงใดๆเกิดจากการ ประกอบกันของชิ้นส่วนเล็กๆจำนวนมากมาย (infinity) ในบทนี้เราจะศึกษา เกี่ยวกับ

การประมาณค่าพื้นที่
The definite integral
ทฤษฎีเบื้องต้น และทฤษฎีพื้นฐานของแคลคูลัส

5.2.2 การประมาณค่าพื้นที่และปริพันธ์จำกัดเขต

พิจารณาฟังก์ชัน \(y=f(x) \ge 0\) บนช่วงเปิด \([a,b]\) ถ้าเราต้องการประมาณค่าพื้นที่ที่ล้อมรอบด้วยส่วนโค้ง \(y=f(x)\) แกน \(x\) และเส้นตรง \(x=a\;,\;x=b\)

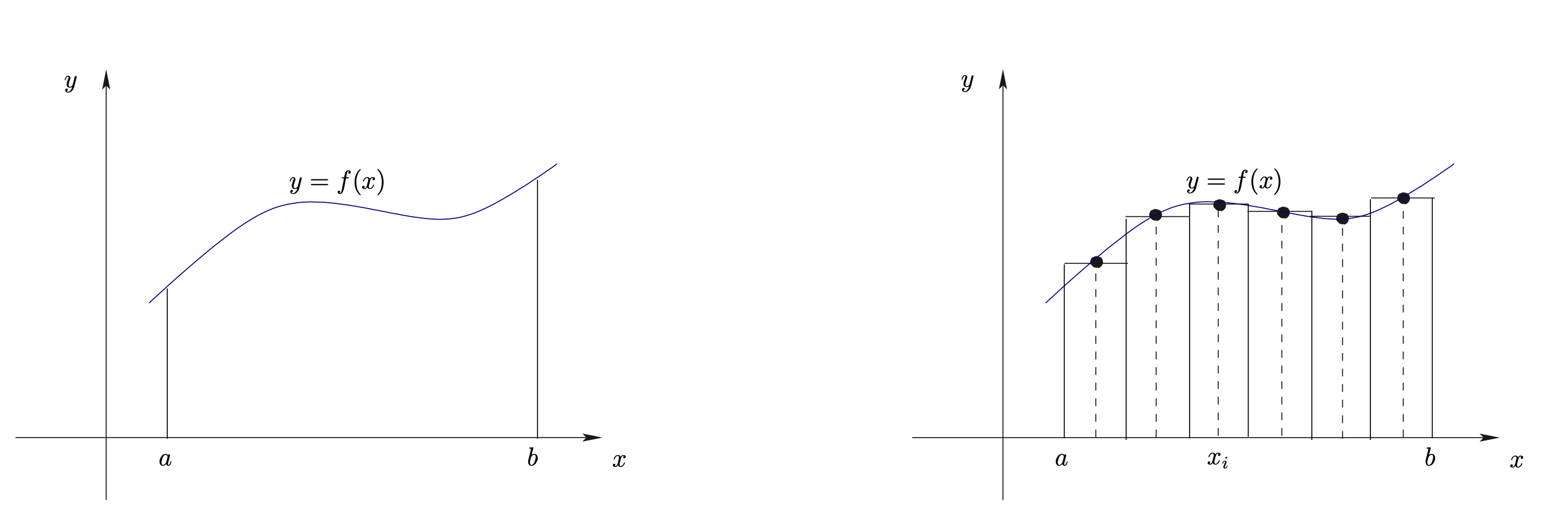
Figure 5.1: การประมาณค่าพื้นที่

วิธีการหนึ่งที่ทำได้ก็คือ การหาผลรวมของพื้นที่รูปสี่เหลี่ยมผืนผ้าที่มาประกอบกันคุมพื้นที่ดังรูป ยิ่งขนาดของรูปสี่เหลี่ยม ผืนผ้าเล็กมากๆ ความถูกต้องของการประมาณค่าจะยิ่งใกล้เคียงค่าจริงยิ่งขึ้น แนวคิดเกี่ยวกับการประมาณค่าโดยอาศัยรูปสี่เหลี่ยมผืนผ้านั้นเป็นวิธีการพื้นฐานที่ใช้ในการคำนวณหาพื้นที่ใต้ส่วนโค้ง การหาพื้นที่ \(A\) ที่ล้อมรอบด้วย ส่วนโค้ง \(y=f(x)\) แกน \(x\) และเส้นตรง \(x=a\;,\;x=b\) เราต้องแบ่งช่วง \([a,b]\) ออกเป็น \(n\) ช่วงเล็กๆขนาด เท่ากันคือ \(\frac{b-a}{n}\) สำหรับ \(I=0,1,2,…,n-1\) ลากเส้นตรงแนวดิ่งตัวส่วนโค้งและสร้างรูปสี่เหลี่ยมผืนผ้าทางด้านขวาของ เส้นตรงแนวดิ่งนี้ จะได้ว่าความสูงของสี่เหลี่ยมผืนผ้ารูปที่ \(I\) คือ \(f(x_i)\) และ พื้นที่ของสี่เหลี่ยมผืนผ้ารูปที่ \(\;I\;\) คือ \(\;\;\frac{b-a}{n}\times f(x_i)\;\;\) ดังนั้น พ.ท.ทั้งหมดของสี่เหลี่ยมผืนผ้า \(n\) รูป คือ \[A(n)= \sum_{i=0}^{n-1}\frac{b-1}{n}f(x_i)\] โดยที่ \(x_i = a + \frac{i}{n}(b-a)\)

ขณะที่จำนวนของช่วงย่อยต่างๆเพิ่มขึ้น ขนาดของช่วงย่อยเหล่านี้คือ \(\frac{b-a}{n}\) จะลดลง และพื้นที่ \(A(n)\) จะเข้าใกล้ พื้นที่ \(A\) ที่เราต้องการคำนวณ ดังนั้นพื้นที่ \(A\) สามารถหาค่าได้จากสมการข้างล่างนี้ \[A= \lim\limits_{n\rightarrow\infty}\sum_{i=0}^{n-1}\frac{b-a}{n}f(x_i)\]

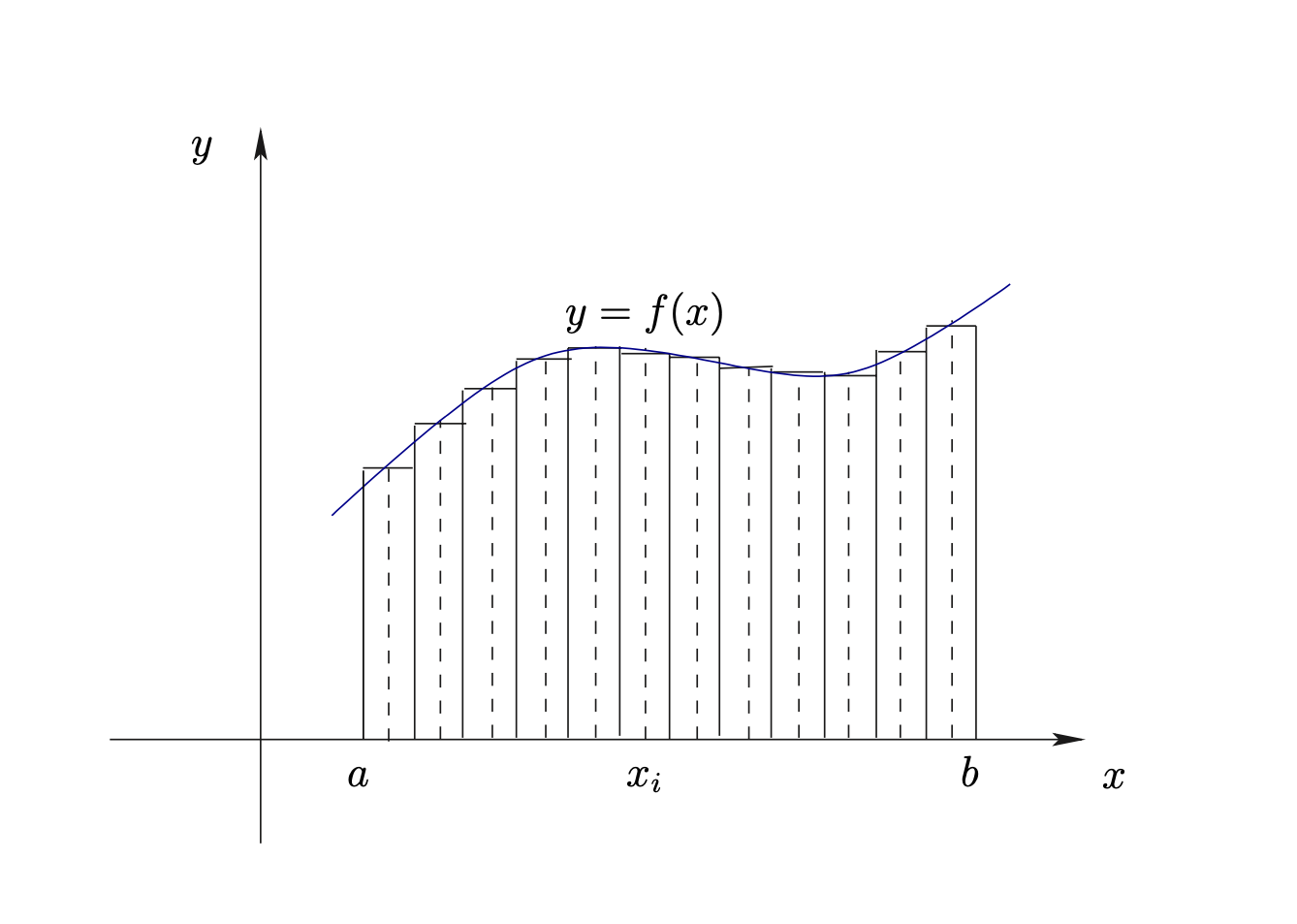
Figure 5.2: การประมาณค่าพื้นที่ใต้เส้นโค้งโดยอาศัยการสร้างสี่เหลี่ยมผืนผ้า

ถ้าเรากำหนดให้ \(\Delta x=\frac{b-a}{n}\) นิยามของการ integrate คือ \(\int^b_af(x)dx= \lim\limits_{\Delta\rightarrow 0}\sum_a^bf(x_i)\Delta x\)
โดยที่ \(a\) และ \(b\) เป็นลิมิตของการอินทิเกรท และสัญลักษณ์ \(\int^b_af(x)dx\) เป็นจำนวน ไม่ใช่ฟังก์ชัน และเรียกสัญลักษณ์นี้ว่า definite integral

ตัวอย่าง 5.3 จงคำนวณหาพื้นที่ ที่ล้อมรอบด้วยส่วนโค้ง \(y=x^2\) เส้นตรง \(x=0,x=4\) และแกน \(x\)

วิธีทำ สูตรสำหรับประมาณค่าพื้นที่ คือ \(\sum_{i=0}^{n-1}\frac{b-a}{n}f(x_i)\)

กรณีที่ 1 : ใช้รูปสี่เหลี่ยมผืนผ้า 4 รูป

เรามี \(f(x)=x^2\;\;,\;\;a=0\;\;,\;\;b=4\;\;,\;\;n=4\;\;\;\) และ

\(x_0=0\;\;,\;\;x_1=1\;\;,\;\;x_2=2\;\;,\;\;x_3=3\;\;\) จะได้ว่า
พื้นที่โดยประมาณคือ

\([1\times (0)^2]+[1\times (1)^2]+[1\times (1)^2]+ [1\times (3)^2]\)

\(=[0]+[1]+[4]+[9]=14\)

กรณีที่ 2 : ใช้รูปสี่เหลี่ยมผืนผ้า 8 รูป
พื้นที่โดยประมาณคือ

\([1\times (0)^2]+[0.5\times (0.5)^2]+[0.5\times (1)^2]+ [0.5\times (1.5)^2]+ [0.5\times (2)^2]+ [0.5\times (2.5)^2]+ [0.5\times (3)^2]= [0.5\times (3.5)^2]\)
\(=[0]+[0.125]+[0.5]+[1.125]+[2]+[3.125]+[4.5]+[6.125]=17.5\)

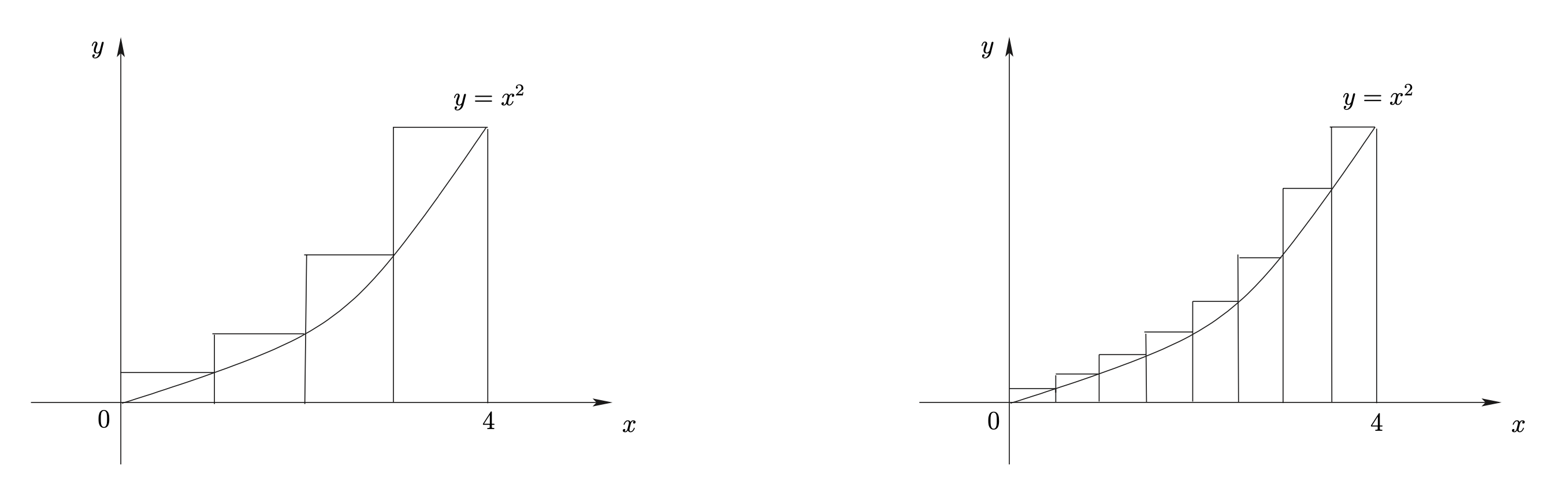
Figure 5.3: การประมาณค่าพื้นที่ใต้เส้นโค้ง ระหว่าง \(x=0\) และ \(x=4\) และอยู่เหนือแกน \(x\)

5.3 ทฤษฎีพื้นฐานของแคลคูลัส (The fundamental Theorem of Calculus)

วิชาแคลคูลัสแบ่งออกเป็น 2 สาขา คือ แคลคูลัสที่เกี่ยวกับการหาอนุพันธ์ ซึ่งถือกำเนิดมาจากความต้องการที่จะหาความชันของฟังก์ชัน และแคลคูลัส ที่เกี่ยวกับการอินทิเกรท ซึ่งถือกำเนิดมาจากความต้องการที่จะหาพื้นที่ใต้กราฟ

ทฤษฎีพื้นฐานของแคลคูลัสเป็นทฤษฎีที่เป็นตัวเชื่อมระหว่าง 2 สาขาทางแคลคูลัส และใช้แสดงความเกี่ยวเนื่องของการหา antiderivative ของฟังก์ชันหนึ่งกับการคำนวณหา definite integral ของฟังก์ชันนั้น \[\int^b_af(x)dx= \lim\limits_{\Delta\rightarrow 0}\sum_a^bf(x_i)\Delta x\] เราใช้สัญลักษณ์ \(\int f(x)dx\) แทน antiderivative ของฟังก์ชัน \(f(x)\) และเรียกสัญลักษณ์นี้ว่า indefinite integral

ทฤษฎี 5.1 \(( \mbox{ทฤษฎีพื้นฐานของแคลคูลัส})\) ถ้า \(f\) เป็นฟังก์ชันต่อเนื่องในช่วง \([a,b]\) แล้ว

ถ้า \(\displaystyle g(x)=\int_{a}^{x}f(t) \ dt\) แล้ว \(g'(x)=f(x)\)
\(\displaystyle \int_{a}^{b}f(x) \ dx=F(b)-F(a)\) เมื่อ \(F\) คือ antiderivative ของ \(f\)

ข้อสังเกต ข้อสรุป 1. ในทฤษฎีข้างต้นสามารถเขียนในรูป

\(\displaystyle \frac{d}{dx}\left(\int_{a}^{x}f(t) \ dt\right)=f(x)\)

ตัวอย่าง 5.4 จงหาอนุพันธ์ของ \(\displaystyle g(x)=\int_{0}^{x}\sqrt{1+t^{4}} \ dt\)

วิธีทำ เนื่องจาก \(\displaystyle f(t)=\sqrt{1+t^{4}}\) เป็นฟังก์ต่อเนื่อง

ดังนั้น จากทฤษฎีพื้นฐานของแคลคูลัส \(\displaystyle \frac{d}{dx}\left(g(x)\right)=\sqrt{1+x^{4}}\)

ตัวอย่าง 5.5 จงหา \(\displaystyle \frac{d}{dx}\int_{0}^{x^{2}}\sin t \ dt\)

วิธีทำ ให้ \(U=x^{2}\) ดังนั้น

\(\qquad \qquad \ \displaystyle \frac{d}{dx}\int_{0}^{x^{2}}\sin t \ dt =\frac{d}{dx}\int_{0}^{U}\sin t \ dt\)

\(\qquad \qquad \qquad \qquad \qquad \quad =\displaystyle \frac{d}{dU}\left(\int_{0}^{U}\sin t \ dt\right) \frac{dU}{dx} \quad ( \mbox{โดยกฎลูกโซ่})\)

\(\qquad \qquad \qquad \qquad \qquad \quad =\displaystyle \sin U \, \frac{dU}{dx} \quad ( \mbox{โดยทฤษฎีพื้นฐานทางแคลคูลัส} )\)

\(\qquad \qquad \qquad \qquad \qquad \quad =\displaystyle \sin x^{2}\cdot 2x\)

\(\qquad \qquad \qquad \qquad \qquad \quad =\displaystyle 2x\cdot \sin x^{2}\)

ตัวอย่าง 5.6 จงหา \(\displaystyle \int_{0}^{2}e^{x} \ dx\) โดยใช้ทฤษฎีพื้นฐานทางแคลคูลัส

วิธีทำ เนื่องจาก \(F(x)=e^{x}\) เป็น antiderivative ของ \(f(x)=e^{x}\) และ \(f(x)\) เป็นฟังก์ต่อเนื่อง ในช่วง \([0,2]\)

ดังนั้น \(\displaystyle \int_{0}^{2}e^{x}\ dx = F(2)-F(0) =e^{2}-e^{0} = e^{2}-1\)

5.3.1 สูตรพื้นฐานของการอินทิเกรท (Basic Integration Rules)

จากทฤษฎีพื้นฐานทางแคลคูลัส (The fundamental Theorem of Calculus) เราทราบว่า ถ้า \(\displaystyle g(x)=\int_{a}^{x}f(t) \ dt\) แล้ว \(g'(x)=f(x)\) และจากนิยามของ antiderivative เราสรุปได้ว่า \(\displaystyle g(x)=\int_{a}^{x}f(t) \ dt\) เป็น antiderivative ของ \(f(x)\) ซึ่งเรามักจะเขียน \(\displaystyle \int f(x) \ dx\) แทน antiderivative ของ \(f(x)\)

นั่นคือ

จากเนื้อหาเรื่องการหาอนุพันธ์ของฟังก์ชันเราทราบว่า \(\displaystyle \frac{d}{dx} \left( \ln |x|+C \right)=\frac{1}{x}\) , เมื่อ \(C\) เป็นค่าคงที่

ดังนั้นจากคำอธิบายในข้างต้น เราสรุปได้ว่า

\[\displaystyle \int \frac{1}{x} \ dx = \ln|x|+C\]

ในทำนองเดียวกัน เราสามารถใช้ความรู้เรื่องการหาอนุพันธ์สร้างสูตรพื้นฐานของการอินทิเกรทได้ดังนี้

\(\displaystyle \int C f(x) \ dx = C \int f(x) \ dx\) เมื่อ \(C\) เป็นค่าคงที่
\(\displaystyle \int [f(x)+g(x)] \ dx = \int f(x) \ dx+\int g(x) \ dx\)
\(\displaystyle \int k \ dx = kx+C \quad\) เมื่อ \(k, C\) เป็นค่าคงที่
\(\displaystyle \int x^{n} \ dx = \frac{x^{n+1}}{n+1}+C \quad\) เมื่อ \(n\neq -1\)
\(\displaystyle \int \frac{1}{x} \ dx = \ln|x|+C\)
\(\displaystyle \int e^{x} \ dx = e^{x}+C\)
\(\displaystyle \int a^{x} \ dx = \frac{a^{x}}{ \ln a}+C \quad\) เมื่อ \(a\) เป็นจำนวนบวก และ \(a\neq 1\)
\(\displaystyle \int \sin x \ dx = -\cos x+C\)
\(\displaystyle \int \cos x \ dx = \sin x+C\)
\(\displaystyle \int \sec^{2} x \ dx = \tan x+C\)
\(\displaystyle \int \csc^{2} x \ dx = -\cot x+C\)
\(\displaystyle \int \sec x \tan x \ dx = \sec x+C\)
\(\displaystyle \int \csc x \cot x \ dx = -\csc x+C\)
\(\displaystyle \int \frac{1}{x^{2}+1} \ dx = \arctan x+C\)
\(\displaystyle \int \frac{1}{\sqrt{1-x^{2}}} \ dx = \arcsin x+C\)

ตัวอย่าง 5.7 จงหา \(\displaystyle \int (9x^{5}-4 \csc^{2} x) \ dx\)

วิธีทำ

\(\qquad \qquad \ \displaystyle \int (9x^{5}-4 \csc^{2} x) \ dx \ = 9\int x^{5} \ dx -4 \int \csc^{2} x \ dx \quad ( \mbox{สูตร} \ 1 \ \mbox{และ} \ 2)\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \quad \ \ =\displaystyle \frac{9}{ 6}x^{6} -4(-\cot x)+C \quad ( \mbox{สูตร} \ 4 \ \mbox{และ} \ 11)\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \quad \ \ =\displaystyle \frac{3}{2}x^{6}+4\cot x+C\)

ตัวอย่าง 5.8 จงหา \(\displaystyle \int \frac{\cos \theta}{\sin^{2} \theta} \ d\theta\)

วิธีทำ

\(\qquad \qquad \ \displaystyle \int \frac{\cos \theta}{\sin^{2} \theta} \ d\theta \ = \int \left(\frac{1}{\sin \theta}\right) \left(\frac{\cos \theta}{\sin \theta}\right) \ d\theta\)

\(\qquad \qquad \qquad \qquad \qquad = \displaystyle \int \csc \theta \cot \theta \ d\theta\)

\(\qquad \qquad \qquad \qquad \qquad = \displaystyle -\csc \theta +C \quad ( \mbox{สูตร} \ 13)\)

ตัวอย่าง 5.9 จงหา \(\displaystyle \int \frac{x^{3}+2\sqrt{x}-3}{x^{\frac{3}{2}}} \ dx\)

วิธีทำ จะเห็นว่า \(\displaystyle \frac{x^{3}+2\sqrt{x}-3}{x^{\frac{3}{2}}} \ = \ \frac{x^{3}}{x^{\frac{3}{2}}}+\frac{2\sqrt{x}}{x^{\frac{3}{2}}}-\frac{3}{x^{\frac{3}{2}}}\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ = \ x^{\frac{3}{2}}+2x^{-1}-3x^{-\frac{3}{2}}\)

\(\qquad \qquad\ \displaystyle \int \frac{x^{3}+2\sqrt{x}-3}{x^{\frac{3}{2}}} \ dx \quad \ = \int x^{\frac{3}{2}} \ dx +2 \int x^{-1} \ dx -3 \int x^{-\frac{3}{2}} \ dx\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ =\displaystyle \frac{x^{\frac{3}{2}+1}}{\frac{3}{2}+1} + 2 \ln |x| -\frac{3x^{-\frac{3}{2}+1}}{-\frac{3}{2}+1} + C\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ =\displaystyle \frac{x^{\frac{5}{2}}}{\frac{5}{2}} + 2 \ln |x|-\frac{3x^{-\frac{1}{2}}}{-\frac{1}{2}}+ C\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ =\displaystyle \frac{2}{5}x^{\frac{5}{2}}+ 2 \ln |x|+\frac{6}{\sqrt{x}}+ C\)

ตัวอย่าง 5.10 จงหา \(\displaystyle \int_{0}^{1} \left( x^{4} - \frac{2}{1+x^{2}} \right) \ dx\)

วิธีทำ

\(\qquad \qquad\ \displaystyle \int_{0}^{1} \left( x^{4} - \frac{2}{1+x^{2}} \right) \ dx \ = \int_{0}^{1} x^{4} \ dx - 2 \int_{0}^{1} \frac{1}{1+x^{2}} \ dx\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ =\displaystyle \frac{x^{5}}{5} \bigg |_{0}^{1}-2 \arctan x \bigg |_{0}^{1}\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ = \displaystyle \left( \frac{1}{5} - 0 \right) - 2 \left( \arctan 1 - \arctan 0 \right)\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ =\displaystyle \frac{1}{5}-2 \left( \frac{ \pi }{4}-0 \right)\)

\(\qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ =\displaystyle \frac{1}{5}- \frac{ \pi }{2}\)